Playlist
Show Playlist
Hide Playlist
Non-competitive Reversible Inhibition – Enzyme Inhibitors
-
03 Advanced Enzymes&Kinetics3.pdf
-
Reference List Biochemistry.pdf
-
Download Lecture Overview
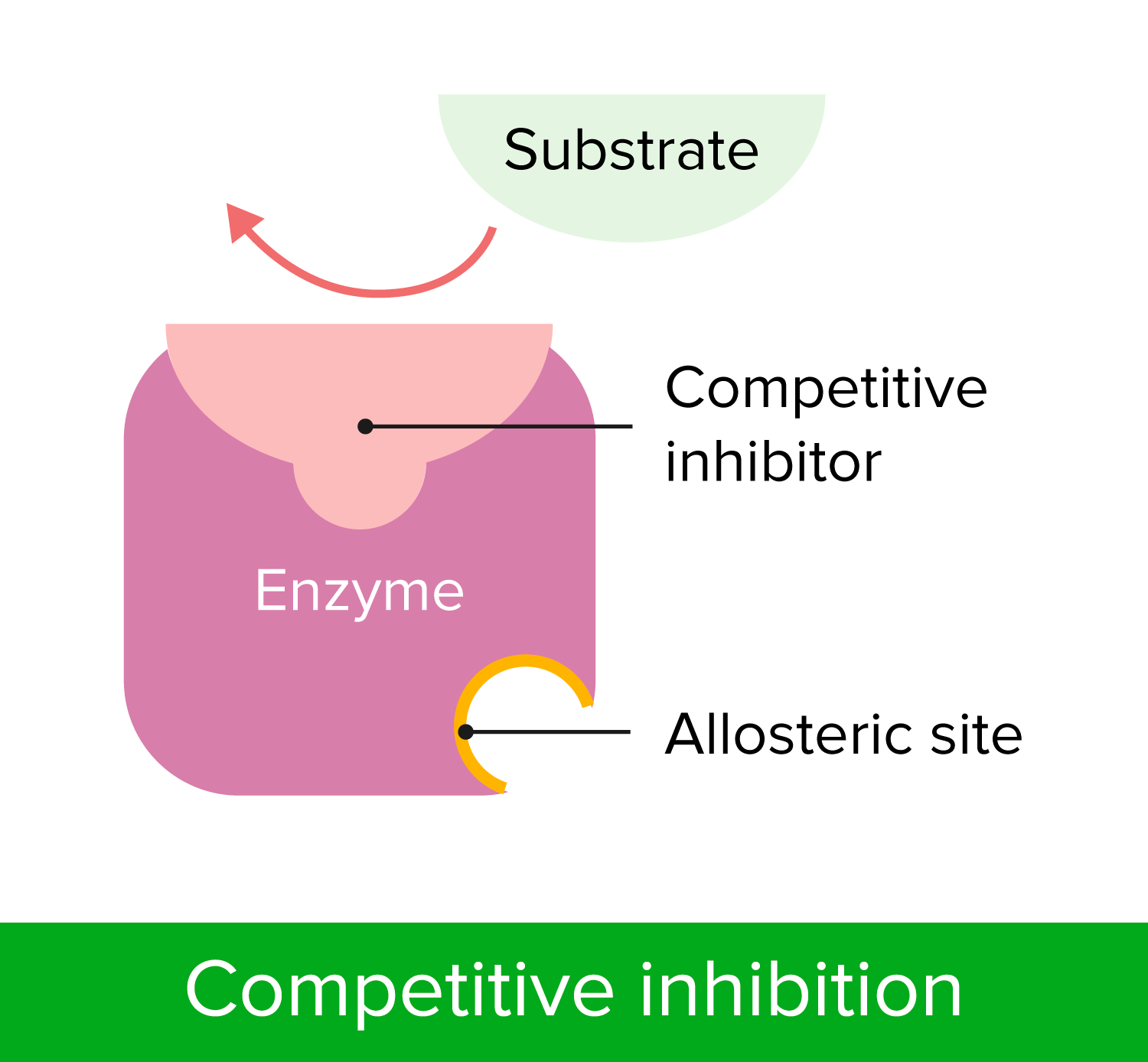
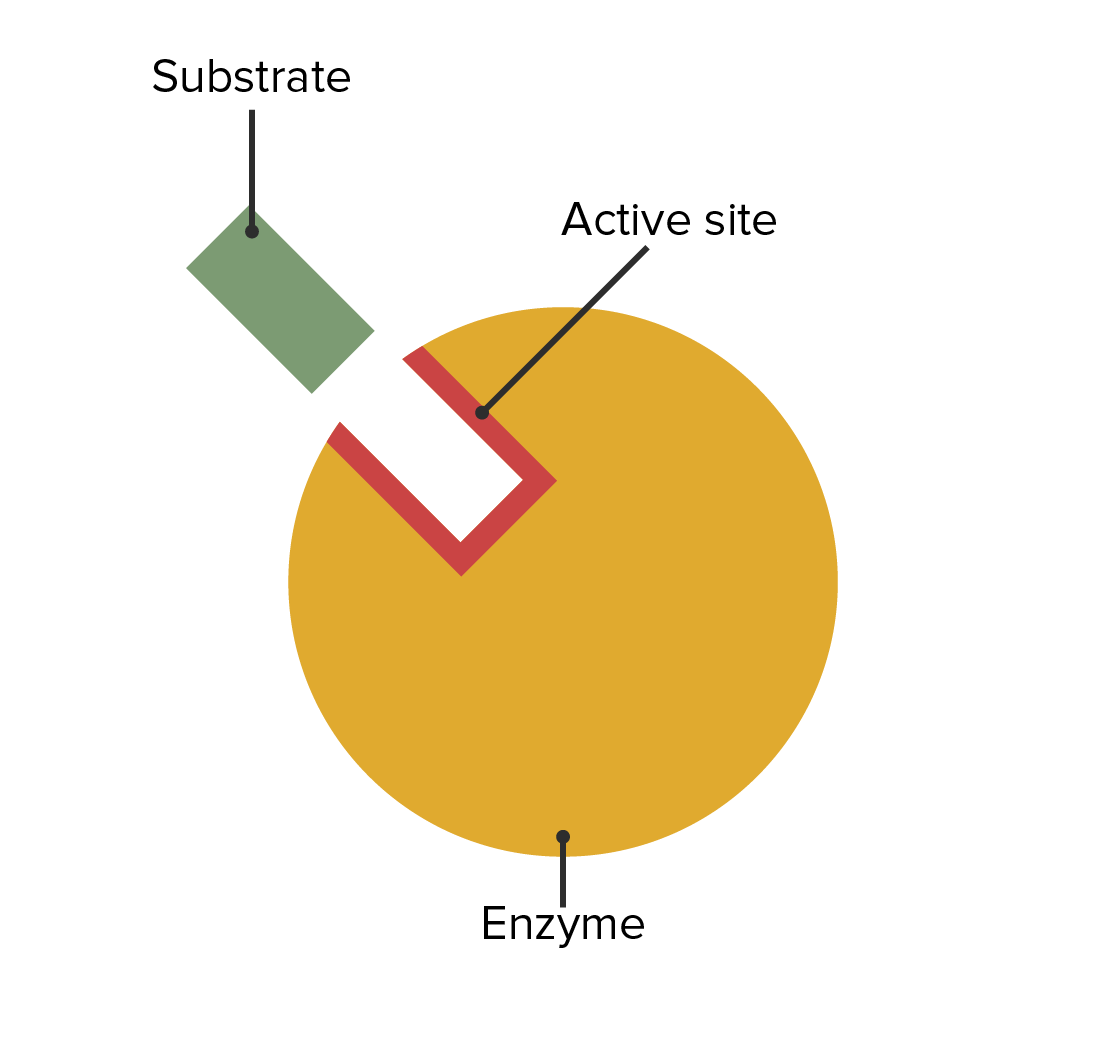
00:01 Eine andere Art der Hemmung, die wichtig für uns ist, zu verstehen, ist die nicht-kompetitive Hemmung. 00:05 Sie ist grundlegend anders als die kompetitive Hemmung und hier auf dem Bildschirm dargestellt. 00:10 Auf der linken Seite haben wir wieder das Enzym mit seinem normalen Substrat, das eine Reaktion katalysiert. 00:15 Das Enzym hat jedoch eine bestimmte Stelle. Wenn diese von einem Inhibitor korrekt anvisiert wird, kann er daran binden und das Enzym daran hindern, richtig zu funktionieren, wenn sich das Substrat im aktiven Zentrum befindet. Dies ist auf dem Bild rechts zu sehen. 00:30 Dieser nicht-kompetitive Hemmstoff hat eine grundlegend andere Art der Wechselwirkung mit dem Enzym, als wir es zuvor gesehen haben. 00:39 Er bindet an einen anderen Ort und durch die Bindung an einen anderen Ort konkurriert er nicht, okay? Dies ändert die Parameter der Reaktionsgeschwindigkeit, die wir untersucht haben, erheblich. 00:52 Und weil der Inhibitor nicht mit dem Substrat konkurriert und das Substrat ihn nicht durch eine Reaktion mit noch viel mehr Substrat übertreffen kann, bedeutet das, dass bei jeder Reaktion, die wir durchführen, wir eine vorgegebene Menge eines Enzyms hemmen. 01:12 Es spielt keine Rolle, wie viel Enzym wir hinzufügen, es wird immer die gleiche Menge Enzyme gehemmt. 01:17 Bei den ersten Reaktionen - den kompetitiv gehemmten Reaktionen - sahen wir, dass mit der Zugabe von mehr Substrat der Inhibitor verdrängt wurde und es schien, als würde der Inhibitor verschwinden. 01:29 Die Menge des gehemmten Enzyms änderte sich also: Je mehr Substrat wir hinzufügten, desto mehr normales Enzym erhielten wir. 01:37 Mit einem nicht-kompetitiven Inhibitor ist das nicht der Fall. 01:39 Es spielt keine Rolle, wie viel Substrat wir haben, denn sie konkurrieren nicht um die gleiche Stelle. 01:43 Der nicht-kompetitive Inhibitor wird immer die gleiche Menge Enzym ausschalten - in jedem Röhrchen, unabhängig davon, wie viel Substrat zugegeben wird. 01:55 Das bedeutet, dass wir die die Menge des Enzyms verändert haben. 01:58 Und wenn wir die Menge des Enzyms ändern, haben wir bereits über die Grenzen gesprochen bei der Untersuchung von Vmax. 02:05 Erinnern Sie sich an den Vergleich mit der Fabrik? Da habe ich gesagt, dass eine zusätzliche Fabrik die Menge des Produkts verdoppeln würde. 02:12 Was wäre, wenn die Fabrik nur einen halben Tag arbeiten würde? Wenn die Fabrik nur einen halben Tag arbeiten würde, würde sie die halbe Menge Produkt herstellen. 02:20 Wir haben die Anzahl der Arbeiter geändert. 02:22 Was passiert also, wenn wir genug Inhibitor verwenden, sodass wir nur die halbe Menge Enzym haben? Nun, wir werden Vmax entsprechend verändern. 02:28 Wenn wir also einen nicht-kompetitiven Inhibitor haben, verändern wir die Menge des Enzyms, und durch die Änderung der Enzymmenge haben wir den Wert von Vmax verändert. 02:38 Vmax sinkt also bei einem nicht-kompetitiven Inhibitor. 02:42 Das war nicht der Fall bei einem kompetitiven Inhibitor, richtig? Nun, wir können Km nur für ein aktives Enzym messen. 02:48 Und, nicht überaschend, wenn wir die Menge des Enzyms verändern, ändert sich Km - die Affinität des Enzyms für das das Substrat - nicht, denn das Enzym ist immer noch das Enzym, wenn es aktiv ist und wir betrachten hier nur aktive Enzyme. Der Km-Wert ändert sich also nicht bei der nicht-kompetitiven Hemmung. 03:06 In einem Lineweaver-Burk-Diagramm sehen wir etwas anderes als bei der kompetitiven Hemmung; aber es stimmt mit dem überein, was ich Ihnen eben erzählt habe. 03:14 In Grün sehen wir wieder die Gerade, die die ungehemmte Reaktion zeigt. 03:21 In Blau sehen wir die nicht-kompetitiv gehemmte Reaktion und wir bemerken, dass die beiden Linien sich bei -1/Km schneiden. 03:29 Dies stimmt mit dem überein, was wir im letzten Diagramm gelernt haben, nämlich dass der Km-Wert sich nicht ändert. Sie sollten sich an diesem Punkt schneiden. 03:35 Wir sehen jedoch, dass die blaue Gerade einen höheren Anstieg als die grüne Gerade hat, was bedeutet, dass der Schnittpunkt mit der y-Achse an einem höheren Punkt liegt. 03:47 Nun mag es kontraintuitiv erscheinen dass, wenn wir Vmax verringern, wir tatsächlich die Werte auf dieser Geraden erhöhen. Aber denken Sie daran, dass es sich um reziproke Werte handelt. 03:56 Durch die Verringerung von Vmax erhöht sich also 1/Vmax.
About the Lecture
The lecture Non-competitive Reversible Inhibition – Enzyme Inhibitors by Kevin Ahern, PhD is from the course Enzymes and Enzyme Kinetics.
Included Quiz Questions
In non-competitive inhibition of an enzyme, which of the following is true?
- The Km value remains unaffected in the presence of the inhibitor, but the Vmax decreases.
- The Km value increases and Vmax decreases.
- Km value and Vmax both increase.
- Both Km and Vmax remain unaffected.
- The Km value decreases and, Vmax increases.
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
5 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |