Playlist
Show Playlist
Hide Playlist
Testing Hypotheses about Proportions
-
Slides Statistics pt2 Testing Hypotheses about Proportions.pdf
-
Download Lecture Overview
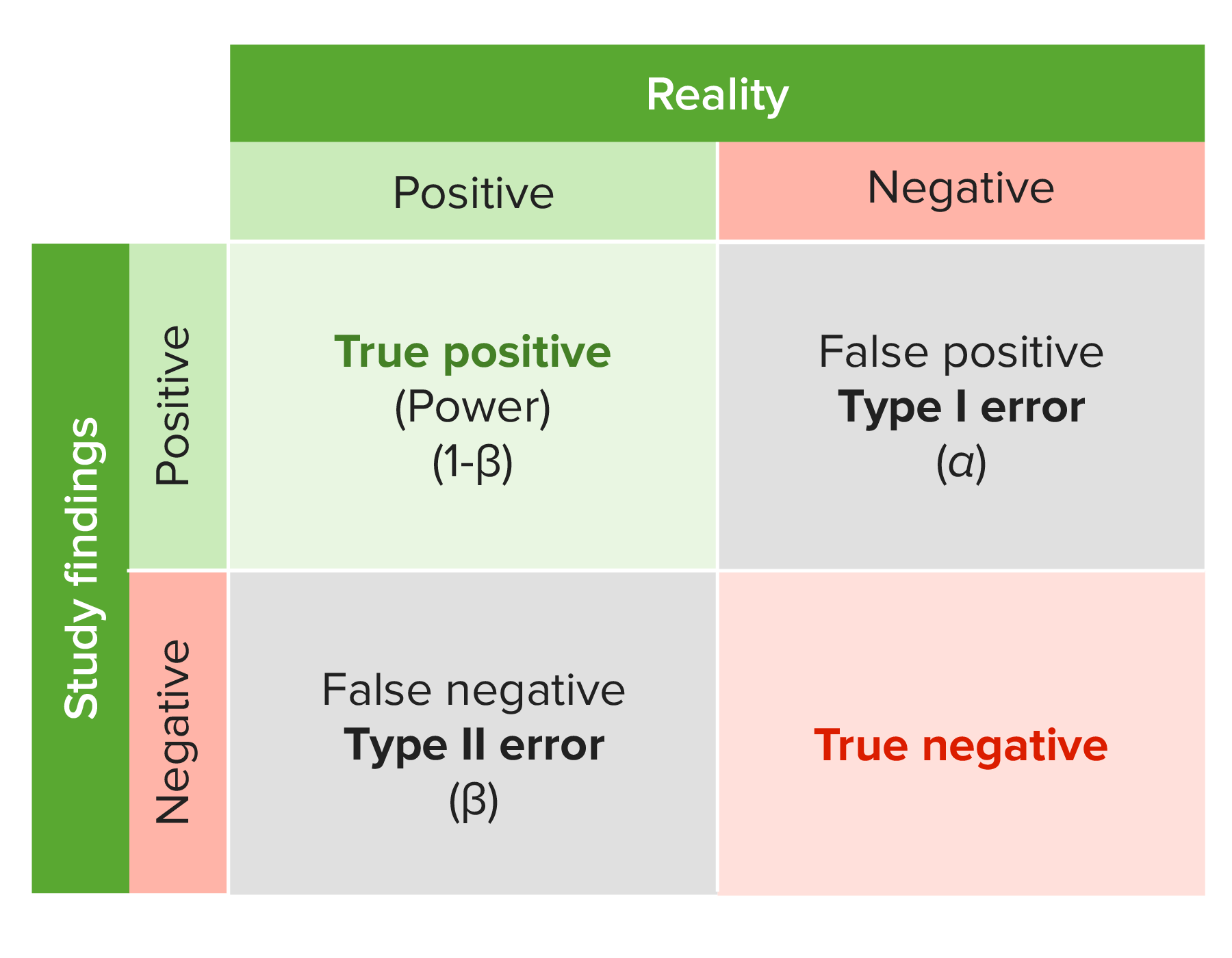
00:01 Welcome back for lecture 3 in which we discuss testing hypothesis about proportions. 00:07 So let's start with an example to motivate what it is that we're trying to do in this lecture. 00:11 Suppose that in a particular college level mathematics course, it's known that 20% of the students are earning a grade of D or F or they're just withdrawing from the course The department of mathematics has decided to redesign the course in the hopes of decreasing the percentage of students that get a D or F or withdraw. 00:27 After a year of the redesigned course, the department randomly selects the records of 400 students and find that in the sample, 17% of them had a D or an F or they withdrew. 00:37 The question is, should the department continue with the redesign, conclude that the redesign is a success or is this lower rate in the sample simply due to chance? So to answer these kinds of questions, we test hypothesis about statistical models. 00:54 So how do we set up hypothesis? Well what we're doing is we're setting up a probability model. 00:59 So in setting up the hypothesis, what we wanna do is we wanna see if a change or an effect has taken place. 01:05 And in order to do that, we first assume that it hasn't and then we let the data try to convince us otherwise. 01:11 We temporarily adapt this assumed model and then evaluate it once we have the data. 01:17 This starting hypothesis is called the null hypothesis and it's called this because it's the assumption that no change has occured. 01:25 In the redesign example, we wanna start by assuming that the percentage of students that withdrew or got a D or an F is still 20% So we write this in the following form : we'll write H0:parameter equals hypothesized value So in this case, if p is the percentage of students with a D or an F or who withdrew, they will write H0: p equals 0.2 We also have an alternative hypothesis,. 01:52 This is what we wanna decide if we conclude the H0 is not plausible. 01:57 So we denote this H1 and what it does is it contains the values of the population parameter that we consider plausible if we decide that H0 is not true. 02:07 In the redesign example, we're interested in reducing the rate of these Fs and withdrawals. 02:13 So our alternative hypothesis then will be written H1: p1 less than 0.2 Otherwise stated, the alternative hypothesis represents what you would want to conclude if you decide that the null hypothesis is not true. 02:28 So how do we decide? What makes us say that the null hypothesis is false? Well let's take a closer look. 02:35 If the new rate of these Fs and withdrawals was 2%, we would probably say that the redesign has worked. 02:41 If the new rate were 19.9%, we might not be as inclined to say that because the difference is easily attributable to chance. 02:50 Our goal is not to determine whether the sample proportion differs from a hypothesized value of proportion, it probably will. 02:57 But the question is, is it a statistically significant difference from the population proportion? If it is, we will conclude that the null hypothesis is likely false. 03:09 So we need to satisfy some conditions before we can perform a hypothesis test. 03:14 So when can we use the procedures that we're about to describe? Well, just like we've had in any other thing we've known at proportions, we need to verify the success/failure condition. 03:25 So what we do is we let.. 03:27 Let's let p0 denote the hypothesized value of a population proportion and let's let n denote the sample size. 03:34 Then what we need to have happened is we need n times our hypothesizd proportion can be at least 10 and we need n times 1 minus our hypothesized value to be at least 10. 03:44 If this condition holds, then we can approximate the distribution of a sample proportion with a normal distribution that has mean p0 and standard deviation p0 times 1 minus p0 over n. 03:58 Why is this a standard deviation in this example and not a standard error like it was for confidence intervals? Well, here we're not estimating the population proportion, we're assuming it has a particular value. 04:10 Standard error's a term that we reserve for when we estimate the standard deviation. 04:15 Let's start with an example. 04:18 If the null hypothesis is true, if 20% of students are getting D's, F's or withdrawing from the course, before we can proceed we first need to check the success/failure condition. 04:28 Our hypothesized value of the proportion is 0.2 So we have, we sampled 400 students, so we have n p0 equals 400 times .2 which is 80, which is much bigger than 10 and then we have n times 1 minus p0 equals 400 times 0.8 or 320 which is also much bigger than 10 So we're good on the success/failure condition. 04:51 What that means is that our sample proportion has a normal distribution with mean p equals .2 and standard deviation square root of p01 minus p0 over n or square root of .2 times .8 over 400 which is 0.02 The question becomes then, is the sample proportion of 0.17 rare given the assumption that the population proportion is 0.2? So we answer this question by finding the probability of observing something as extreme or more extreme than what we observed. 05:22 which means as far or farther away from the hypothesized proportion in the direction of the alternative hypothesis. 05:30 So let's try it. 05:31 If the true population proportion is 0.2, then we want the probability that p hat is less than or equal to 0.17 and we can translate that to a z-score and we get the probability that z is less than or equal to .17 minus .2 divided by .02 since .02 is our standard deviation which is equal to the probability that z is less than or equal to minus 1.5 Remember that z is a normal (0,1) random variable. 06:01 So using the table we find that this probability is equal to the probability that z is bigger than or equal to positive 1.5 or 1 minus the probability that z is less than or equal to 1.5 which is 0.067 So what this means is that if the null hypothesis were true, then our sample proportion will be .17 or smaller, 6.7% of the time. 06:24 It's up to the investigator to decide whether this is compelling evidence to conclude that the redesign has been a success We can view our hypothesis test as kind of like a criminal trial, and US criminal law, a defendant is innocent until proven guilty. 06:41 So we can think of a null hypothesis as a presumption of innocence. 06:45 The data are the evidence. 06:48 And the data are judged and evaluated in order to determine whether the null hypothesis is false. 06:53 Jsut like the jury might decide whether the evidence against the defendant were plausible if the defendant were actually innocent At this point, it's up to the jury to make the decision. 07:04 In hypothesis testing, the investigator or the statistician is the jury Juries don't give a verdict of innocent in a criminal trial. 07:13 What they say is "not guilty" and this is because they simply don't have enough evidence to conclude that the defendant is guilty So this is not an acceptance of the presumption of innocence but it's not a rejection of that presumption either. 07:28 In hypothesis testing, we do a similar thing. 07:31 We don't accept the null hypothesis. 07:34 We just do not reject it, we basically do the same thing and say "not guilty" Let's look at p-values. 07:41 These kinda answer the question of whether or not the data that we observed are weird. 07:45 So what is a p-value? How do we use it? Well the p-value tells us how likely the data that we observe are if the null hypothesis were in fact true. 07:54 Formally, the p-value is the probability of seeing data like what we saw or something even more extreme if the null hypothesis were true. 08:03 It's a measure of how surprised we are to observe the data that we did if the null hypothesis is true, So we calculated a p-value in our example. 08:14 That p-value is .067 Small p-values give evidence against the null hypothesis. 08:20 In other words, that means we're surprised to see the data that we saw if the null hypothesis were actually true So two possibilities arise, either the null hypothesis is true and we saw something weird, or the null hypothesis is false. 08:35 In statistics, we conclude the latter when the p-value is small. 08:39 So let's formalize the hypothesis testing procedure. 08:43 First off is to formulate the hypothesis. 08:46 We did this in the first example. 08:48 We said the null hypothesis was p equals 0.2 and we tested that against the alternative hypothesis that p is less than .2 The second step is to decide what probability model we're going to use to carry out the task. 09:02 In the example, we use the normal model The test that we use is called the one-proportion z-test and in order to use this model, we need to make sure that we have some conditions satisfied, So let's look at the conditions. 09:15 The first is the randomization condition. 09:17 The observations have to be drawn at random. 09:19 In the redesign example, this is stated in the problem. 09:22 The 10% condition. 09:24 As it's meant before, this means that the sample size should not exceed 10% of the population size. 09:29 In the redesign example, we're going to assume that more than 4000 students took the course over the last year. 09:35 And we have the success/failure condition which we've already addressed. 09:39 We've verified that that condition holds as we went through the example. 09:43 Step three is the mechanics phase. 09:46 This is where we actually calculate the test statistic. 09:48 Different types of tests have different test statistics. 09:51 Now for the one-proportion z-test, the z-score is the test statistic. 09:56 In the example, the test statistic was z equals minus 1.5 We'll encounter other test statistics later on in the course. 10:04 But from the test statistic, we then calculate the p-value In the example, our p-value was 0.067 Next we make a conclusion. 10:13 In this step, we make a decision on whether or not to reject the null hypothesis. 10:17 Once we've made this decision, the conclusion needs to be stated in the context of the problem. 10:23 So in our example, if we decide to reject the null hypothesis in the redesign example, then what we would say is that we have evidence that the redesign has been succesful in reducing the percentage of Ds, Fs and withdrawals. 10:36 Once this conclusion has been made, the next step is to use the information to decide how to proceed from a practical standpoint. 10:43 So do we continue with the redesign or do we drop it? In this example, The department will likely want to continue with the redesign if they decide to reject the null hypothesis. 10:54 When do you reject the null hypothesis? Well typically we set what's called the significance level, this is the threshold for p-values. 11:02 Typically, what we do is we set a value alpha for a p-value such that if a p-value is less than or equal to that value of alpha, we reject the null hypothesis. 11:11 Otherwise, we don't reject the null hypothesis. 11:14 This threshold is what's known as the significance level. 11:19 So the significance level should be set before step 3 begins. 11:22 Before you do any of the mechanics, you should set your significance level. 11:26 In our example, if our signficance level is 0.1, we would reject the null hypothesis and conclude that the redesign has worked. 11:34 If the siginficance level were .05, we would not reject the null hypothesis because this threshold is smaller than the p-value that we observed Setting the significance level before any mechanics are carried out, it's kinda to check on ourselves because what we're doing is we're ensuring that we're not setting a significance level in such a way that we guarantee that the test works a certain way for us. 11:58 So when we talk about a hypothesis test, what things do we report? Well we report the decision and we report the conclusion The significance level we can report we might choose not to, but the p-value is necessary to report. 12:12 And the reason for that is, there's no need for a significance level because if the p-value's known, it allows the reader or some other third party to make his or her own decision about whether or not tha data support of a particular hypothesis. 12:27 So let's formally describe how we compute p-values. 12:30 We have three possible alternative hypothesis. 12:33 We have the alternative hypothesis that p is less than p0, p greater than p0 or p not equal to p0 And to compute these, we compute the p-value always in the direction of the alternative hypothesis So let's let z be a normal random variable with mean zero and standard deviation 1. 12:53 If the alternative hypothesis is p less than p0, then the p-value is the probability that this normal random variable takes a value less than or equal to what we've observed We refer to this alternative as a left-tailed hypothesis If the alternative hypothesis is p greater than p0, then the p-value is computed by taking the probability that this normal random variable takes a value at least as large as what we observed. 13:19 and we call this alternative a right-tailed hypothesis If the alternative hypothesis is p not equal to p0, in other words we're just looking for a difference, the p-value is the probability that z is less than or equal to the absolute negative absolute value of what we observed plus the probability that z is at least as large as the positive absolute value of what we observed. 13:41 Or we can just write that as 2 times the probability that this normal random variable is at least as large as the absolute value of the test statistic we observed. 13:51 So we put some illustrations in here on the next three slides. 13:55 Here's an illustration of what the left-tail test looks like, the left-tail p-value. 14:00 Suppose our alternative hypothesis is p less than p0, and we observe a test statistic z equals minus 1.75 then the p-value is the probability that a normal (0,1) random variable takes a value no larger than minus 1.75 That value is 0.04006 and that probability shaded in in the graph. 14:25 Iif we do an upper tail test or a right-tail test where the alternative is p greater than p0 and we observed a test statistic value of 1.75 Then the p-value is the probability that z is at least as large as 1.75 This is also 0.04006 and that probability in that region is shaded in in the graph on the left hand side of the slide. 14:48 And finally for the two-tailed alternative, the alternative hypothesis is p not equal to p0 and we observed z equals 1.75 So the p-value is 2 times the probability that the normal (0,1) random variable takes a value at least as large as 1.75 and that probability is 0.08012 So we have the region shaded in in the graph so we have the left-tailed side and the right-tailed shaded in And those probabilities in those regions add up to .08012 So we have a lot of things that could go wrong in hypothesis testing so let's discuss some of the pitfalls to avoid. 15:29 Don't base your hypothesis off what you see in the data. 15:33 Don't make your null hypothesis the thing you want to show. 15:37 This is where your alternative is supposed to be for. 15:40 Don't forget to check the conditions. 15:42 If your conditions aren't satisified, if you don't check them and these conditions aren't actually satisifed, then your hypothesis test isn't going to work very well. 15:51 Do not accept the null hypothesis, what we do is we fail to reject it. 15:56 If you fail to reject the null hypothesis, don't think that a larger sample size will be more likely to lead to rejection All samples are different, and a larger one may or may not lead to a rejection. 16:08 So what did we do in this lecture? Well we talked about how to carry out a hypothesis test for population proportion. 16:15 We also described the conditions under which this hypothesis test is appropriate and we discussed some of the things that can go wrong in hypothesis testing, some mistakes that are commonly made. 16:25 So you avoid these mistakes and follow the mechanics and all the four steps as were described in the previous slides. 16:31 And your hypothesis test will go well for you and it will give you valid conclusions This is the end of lecture 3 and I look forward to seeing you all back for lecture 4.
About the Lecture
The lecture Testing Hypotheses about Proportions by David Spade, PhD is from the course Statistics Part 2. It contains the following chapters:
- Testing Hypotheses About Proportions
- The Success/Failure Condition
- P-Values
- Significance Levels
- Pitfalls to Avoid
Included Quiz Questions
What describes the general procedure for hypothesis testing of proportions?
- We set up our null hypothesis in such a way that it states that no change has taken place, and we try to let the data convince us otherwise.
- We set up our null hypothesis as the thing we want to conclude, and we let the data support this belief.
- We set up our null hypothesis in such a way that it states that no change has taken place, and we let the data support this belief.
- We set up our null hypothesis as the thing we want to conclude, and we look to the data to convince us that the null hypothesis is true.
- We set our null hypothesis as the change we expect, and look at the data to see if this holds true.
What is an appropriate interpretation of a p-value?
- The p-value is the probability of seeing data like what we saw, or even something more extreme, if the null hypothesis is true.
- The p-value tells us the probability that the null hypothesis is true.
- The p-value is the probability of seeing data like what we saw, or even something more extreme, if the alternative hypothesis is true.
- The p-value provides a measure of the strength of the evidence against the alternative hypothesis.
- The p-value provides the chance of repeating the experiment with the same result.
What is not a condition that needs to be satisfied in order to use the one-proportion z-test?
- Our data do not need to be random.
- We need to expect at least 10 successes under the null hypothesis.
- The expected number of failures under the null hypothesis must be at least 10.
- The sample size must be no larger than 10% of the population.
- The data must be random.
What is something we do not report after the hypothesis test is complete?
- We do not report the value of the z-statistic.
- We do not report the decision.
- We do not report the conclusion.
- We do not report the p-value.
- We do not report the confidence interval.
What is an example of a good hypothesis testing practice?
- It is a good hypothesis testing practice to check the conditions for the test before using it to make general statements about the population.
- It is a good hypothesis testing practice to base your hypotheses on what you see in the data.
- It is a good hypothesis testing practice to make your null hypothesis what you want to show to be true.
- It is a good hypothesis testing practice to say that you accept the null hypothesis.
- It is good hypothesis testing practice to reject the null hypothesis.
What p-value would imply rejecting the null hypothesis at the 5% level?
- 0.04
- 0.8
- 0.7
- 0.5
- 0.06
What p-value would imply rejecting the null hypothesis at the 1% level?
- 0.005
- 0.99999
- 0.95
- 0.5
- 0.04
What statistical value would not allow one to reject the null hypothesis if the critical value is 1.96?
- 1.98
- 1.95
- 1.94
- 1.93
- 1.92
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
5 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |