Playlist
Show Playlist
Hide Playlist
More about Hypothesis Tests
-
Slides Statistics pt2 More about Hypothesis Tests.pdf
-
Download Lecture Overview
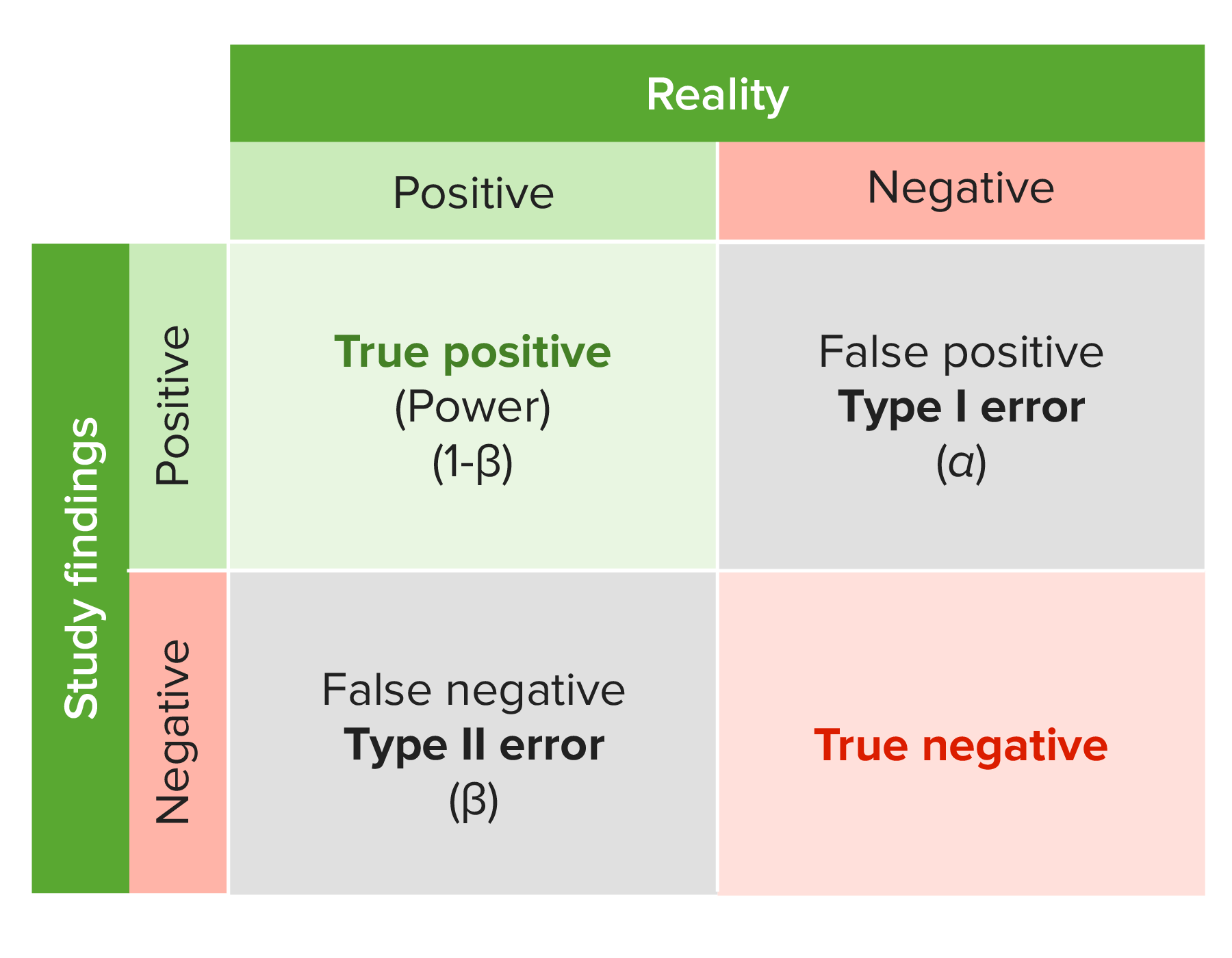
00:01 Welcome back for lecture 4, where we're gonna talk more about hypothesis tests. 00:06 So let's figure out how we choose a null hypothesis and we'll start this with an example. 00:10 Suppose we're interested in the percentage motorcycle riders age 20 years or lower that wear helmets. 00:17 The law in a particular state is changed to require only these riders to wear helmets. 00:22 Before the change, 60% of young riders involved in accidents had been a wearing helmet. 00:27 After the law was changed, a research group observed 781 young riders who were in accidents. 00:33 And of these, only 396 or 50.7% were wearing helmets. 00:38 Has the percentage of the riders in the 20 or younger age group that wear helmets declined or is this a natural fluctuation in the sample proportion? That's the question we wanna ask. 00:48 So now we wanna know how to set up our null hypothesis. 00:51 So how do we do it? Well, remember that usually, the null hypothesis is stated to claim that there is no difference or no effect. 00:59 This does not mean that if p is the percentage of young motorcycle riders that wear helmets, we should assume that p equals 0. 01:06 In fact this would be a silly thing to say. 01:08 Of course there is some people in this group that wear helmets so it would be silly to say that no one wears a helmet in this group. 01:15 In the example, the initial assertion is that the helmet use has not changed. 01:20 Thus we would assume that p equals 0.6 to begin. 01:24 A common temptation is to state the claim as your null hypothesis. 01:29 You wanna resist this temptation. 01:31 The claim you are making and want to prove is what you should put in your alternative hypothesis. 01:37 Remember that we never prove the null hypothesis is true. 01:41 All we do is we collect evidence against it or we collect a lack of evidence against it. 01:46 So now we can think about p-values and let's think about this as a conditional probabilities. 01:51 Because that's exactly what they are. 01:53 The p-value is the probability that we get a result at least as unusual as what we observed given that the null hypothesis is true. 02:01 If this is not and I repeat, NOT the probability that the null hypothesis is true. 02:07 For example, a p-value of 0.02 does not mean that there is a 2% chance that the null hypothesis is right. 02:14 Recall how we looked at the confidence intervals. 02:17 The null hypothesis is about a fixed quantity just like confidence intervals are. 02:22 It's either true or it isn't. 02:24 This is not a random thing, we just don't know which one is the case. 02:28 So what if we have small p-values? What do we do with them? If the p-value is small, this means that if the null hypothesis were true, what we saw is really unlikely. 02:39 So there's two possibilities. 02:41 We saw something really unusual or our initial assumption, the null hypothesis, is wrong. 02:48 In statistics, we conclude that we made a bad assumption. 02:50 We conclude that the null hypothesis is wrong. 02:53 So let's use the motorcycle example. Has helmet use declined? Well the first step, as it always is, is to set up our hypotheses. 03:02 Our null hypothesis being p equals 0.6 versus the alternative that p is less than 0.6. 03:10 Now we have a model that we have to build, so we have to check some conditions. 03:14 The independent/randomization condition, it's reasonable to assume that since these people are randomly sampled, that these individuals are independent of each other. 03:24 We have the 10% condition, 781 riders are less than 10% of the population of young riders. 03:30 We have the success/failure condition. 03:33 We observed 781 people, so n p 0 is 781 times 0.6 or 468.6 which is much larger than 10. 03:42 n times 1 minus p0 is 312.4 which is much larger than 10 as well so we're good on the success/failure condition. 03:51 All the conditions are satisfied, so we can use the one proportion z-test. 03:55 We assume that the sample proportion follows a normal distribution with mean 0.6 and standard deviation square root of .6 times .4 over 781 or 0.0175. 04:10 Now we move on to the mechanics. 04:13 We observe p hat equals 0.507, so our test statistic is z equals 0.507 minus 0.6 divided by the standard deviation of 0.0175, and this gives us a Z of minus 5.31. 04:30 We look at the p-value, the probability that a normal (0,1) random variable takes a value no larger than minus 5.31 is it's smaller than 0.001. 04:42 So what this means is that a sample proportion of 0.507 or smaller happens less than 0.1% of the time if the null hypothesis is actually true. 04:53 So we would reject the null hypothesis. 04:56 What we would say in a practical sense or in context is there's strong evidence that the true percentage of helmet wearers has declined. 05:06 What about large p-values? What do we do with those? Well if the p-value is large then what this tells that is that if the null hypothesis were true, what we saw would not be very surprising. 05:18 For example, in the motorcycle example, if 59% of sampled riders wore helmets, the p-value for that test would be .2839. 05:27 We would observe a sample proportion of 59% or lower 28.39% of the time if the true population proportion of helmet wearers was actually 60%. 05:39 So a sample proportion of 59% does not seem too surprising if the null hypothesis were true. 05:46 So we would not reject the null hypothesis with a p-value this high. 05:50 So in other words, this would not provide strong evidence that the percentage of helmet wearers has declined. 05:56 Let's look at significance levels and how we choose them. 06:00 The answer to the question of what constitutes a reasonable significance level is dependent on the situation. 06:05 The question becomes: What probability do we consider were enough to decide to reject the null hypothesis? The threshold is known as the alpha level or the significance level. 06:18 Common significance levels are 0.01, 0.05 and 0.1 but you can use whatever you want. 06:23 The significance level of 0.05 somehow became kinda the gold standard for the first statistical significance, especially in the social sciences. 06:33 So we talk about statistical significance but what about practical significance? Are they the same thing? Is the difference important? Well the fact that a test statistic is statistically significant does not necessarily mean a practically significant difference. 06:48 For instance we have large sample sizes sometimes and they can result in the rejection of a null hypothesis even when the test statistic is only slightly different from the hypothesized value. 06:58 On the other hand, small sample sizes can result in null hypothesis not being rejected even when the test statistic is quite different from the hypothesized value. 07:08 So the lesson here is to report the magnitude of the difference between statistic and the null hypothesis value along with the p-value. 07:18 The difference may be of practical significance. 07:20 Even if it's not statistically significant or the difference might be of no practical significance even if it is statistically significant. 07:30 Sometimes we make mistakes. So we have a couple types of errors we can make. 07:35 A type I error is when a null hypothesis is true but we reject it anyway. 07:40 A type II error is when a null hypothesis is false but we don't reject it. 07:45 So how do we control the probability of making these types of errors? We set the probability of a type I error when we set our significance level. 07:53 Setting a significance level of 0.05 means that we reject the null hypothesis when it is true 5% of the time. 08:01 Is this too much? If this is too much they we should reduce the significance level. 08:07 What happens when we decrease the significance level? Well this inherently raises the probability of a type II error. 08:14 We're gonna call this probability beta. 08:16 So what's the take away here? Well the take aways is there's a trade off between the probabilities of type I and type II error. 08:23 Reducing the significance level results in an increase in the probability that you're gonna make the other kind of mistake. 08:29 Let's look at the power of the test which is directly related to the type II error. 08:33 What the power of a test is, is the probability that it correctly rejects a false null hypothesis. 08:40 And we denote power 1 minus beta. 08:44 The computation of power depends on the distance between the true value of the population proportion and the hypothesized value of the population proportion. 08:53 For different values of the population proportion, the power will be different. 08:57 Small differences are harder to detect, so we're gonna reject the null hypothesis for small differences less often than we reject the null hypothesis for large differences. 09:07 So for example, we test the same hypothesis as before at the 5% significance level. 09:12 The question is what is the power of a test that the true percentage of young riders that wear helmets is 59%? What about 55%? Well if p equals 0.59, then what we need to do, first we need to find the value of p hat that results in rejection of the null hypothesis. 09:30 Remember that we reject H0 for our test statistic p hat minus 0.6 over 0.0175 takes a value less than or equal to minus 1.645, that's a value that we can find in the z-table. 09:43 So the value of p hat for which we reject the null hypothesis by using some algebra, we find that that value is p hat less than or equal to 0.5712125. 09:54 What we need to do is find the probability that p^ is less than 0.5712125, given that p equals 0.59. 10:04 So what happens if p equals 0.59, then p hat follows a normal distribution with mean 0.59 and standard deviation square root of 0.59 times 0.41 over 781 or 0.0176. 10:22 So then the power is the probability that a normal (0,1) random variable takes a value less than or equal to 0.5712125 minus 0.59 divided by 0.0176. 10:36 In other words this is the probability that a normal (0,1) random variable takes a value less than or equal to minus 1.065 or 0.1434. 10:47 So what that means then is that if the true population proportion is 0.59, then we're gonna reject H0 14.34% of the time. 10:57 So what if the true population proportion is 0.55? Then the sample proportion follows a normal distribution with mean 0.55 and standard deviation 0.0178. 11:10 So the power then is the probability that p hat is less than or equal to 0.5712125, given that p is equal 0.55 which is the probability that a normal (0,1) random variable takes a value less than .5712125 minus 0.55 divided by the standard deviation of .0178 which is the probability that a normal (0,1) random variable takes a value less than or equal to 1.1917 and that probability is 0.08833. 11:44 So what this tells us then is if the true percentage of helmet wearers is 0.55, we're gonna reject the hypothesis p equals 0.6, 88.33% of the time. 11:56 So the power has gone way up because we've moved further away from the hypothesized value. 12:01 The question now becomes, can we increase the power and reduce the type I error probability at the same time. 12:08 And the answer is yes but there's only one way to do it and that's to increase the sample size. 12:13 Sometimes that's not a practical thing to do. 12:16 And sometimes we just kinda have to play the hand that we're dealt in terms of power, type II error and type I error. 12:22 So what can go wrong in hypothesis testing? There are several things that we want to avoid. 12:27 First of all, do not interpret p-values as the probability that the null hypothesis is true. 12:32 That's not what this means. 12:34 The p-value is the probability that if the null hypothesis were true, you observe a test statistic value as wierd or wierder than what you observed. 12:44 Don't believe too much in arbitratry significance levels. 12:48 Usually we use 0.05 but there's little difference between a p-value of .0501 and a p-value 0.0499. 12:59 Don't confuse practical and statistical significance. 13:02 We can make anything statistically significant as long as we have a large enough sample size. 13:07 Don't forget that even though a test is carried out perfectly in terms of mechanics and procedure, we can still be wrong. 13:14 That's a risk that we have to take and that's a risk that we always accept in hypothesis testing. 13:21 So if anybody watches NCIS, we'll look at rule 51, sometimes you're wrong and that's part of the risk of hypothesis testing. 13:30 So what all did we do? We talked about how to carry out our hypothesis test for proportions and we talked about the different types of mistakes that we can make when it comes to hypothesis testing. 13:43 We talked about power and how power increases as the true proportion gets further away from the hypothesized proportion. 13:50 We finished up with some common issues in hypothesis testing, common mistakes that are made and how we can avoid them. 13:57 So this is the end of lecture 4 and I look forward seeing you again for lecture 5.
About the Lecture
hypothesis-testIncluded Quiz Questions
What is true of the null hypothesis?
- The null hypothesis assumes no difference or no effect.
- The null hypothesis for a population proportion is always set at p= 0.
- The null hypothesis is the claim you want to prove.
- The hypothesis test is designed to prove that the null hypothesis is true.
- The null hypothesis is a blank statement.
What is TRUE regarding null hypotheses and p-values?
- The p-value is used to quantify the statistical significance of the results of a hypothesis test.
- The null hypothesis states there is a relationship between the 2 population parameters.
- The null hypothesis states there is statistical significance between the two variables.
- The p-value is the probability that the observed data will reject the null hypothesis.
- The larger the p-value, the stronger the evidence is that you should reject the null hypothesis.
What is the significance level?
- The significance level is the probability that the null hypothesis is rejected when it is true.
- The significance level is the probability that the null hypothesis is rejected.
- The significance level is the probability that the null hypothesis is true.
- The significance level is the probability that the null hypothesis is false.
- The significance level is the amount of importance given by the research community to a study result.
What is true regarding the relationship between the significance level and the power of a test?
- With the sample size staying the same, power increases as the significance level increases.
- With the sample size staying the same, power decreases as significance level increases.
- The power is the probability that the null hypothesis is false, while the significance level is the probability that the null hypothesis is rejected.
- The power is the probability that the null hypothesis is rejected, while the significance level is the probability that the null hypothesis is rejected when it is true.
- An increase in the sample size will have an effect on the power but not the significance level.
What is not true regarding hypothesis testing?
- If the result of our test is statistically significant, this always means that there is significance from a practical standpoint.
- It is possible to carry out a hypothesis test perfectly and still make a mistake.
- The p-value is not to be interpreted as the probability that the null hypothesis is true.
- Increasing the sample size will result in higher power.
- The sample size has an impact on the power of the study.
What is the most widely used significance level?
- 5% significance level
- 1% significance level
- 2% significance level
- 10% significance level
- 15% significance level
90% confidence level is synonymous to which significance level?
- 10% significance level
- 1% significance level
- 2% significance level
- 5% significance level
- 15% significance level
If β is 0.75 then what is the power of the sample?
- 0.25
- 0.2
- 0.3
- 0.35
- 0.4
Customer reviews
5,0 of 5 stars
| 5 Stars |
|
5 |
| 4 Stars |
|
0 |
| 3 Stars |
|
0 |
| 2 Stars |
|
0 |
| 1 Star |
|
0 |