Os testes Testes Gonadal Hormones de diagnóstico são aspetos importantes para fazer um diagnóstico. Certas informações estatísticas sobre a precisão e a validade dos próprios testes Testes Gonadal Hormones podem ajudar a transformar os dados em informação utilizável e aplicável. Alguns dos valores epidemiológicos mais MAIS Androgen Insensitivity Syndrome importantes dos testes Testes Gonadal Hormones diagnósticos incluem a sensibilidade e a especificidade, falsos positivos e falsos negativos, valores preditivos positivos e negativos, razões de verossimilhança e probabilidades pré-teste e pós-teste. Por exemplo, um teste com alta sensibilidade é útil como teste de rastreio, enquanto uma alta especificidade é necessária para um diagnóstico preciso. Alternativamente, valores preditivos positivos e negativos ajudam a determinar a probabilidade de doença no caso de determinados resultados de testes Testes Gonadal Hormones.
Last updated: Jul 28, 2022
Contents
Os testes Testes Gonadal Hormones de rastreio são usados para identificar indivíduos nos estádios iniciais de uma doença e possibilitar a intervenção precoce com o objetivo de reduzir a morbimortalidade.
Os testes Testes Gonadal Hormones de rastreio não fornecem um diagnóstico definitivo:
A utilidade dos testes Testes Gonadal Hormones de rastreio requer a avaliação de:
As tabelas de contingência são usadas frequentemente na análise estatística de múltiplas variáveis. Para avaliar o valor epidemiológico de um teste de rastreio, pode usar-se uma tabela semelhante à apresentada abaixo para determinar as frequências relativas de indivíduos com diferentes combinações de resultados de testes Testes Gonadal Hormones de rastreio (positivos ou negativos) e o estado real de doença (na realidade tem ou não tem a doença).
É importante que a tabela seja disposta de uma forma padronizada para que se possa aplicar fórmulas padrão. A tabela padrão é apresentada abaixo (com os resultados dos testes Testes Gonadal Hormones de rastreio à esquerda, o verdadeiro estado da doença no topo e as respostas “sim” antes das respostas “não”).
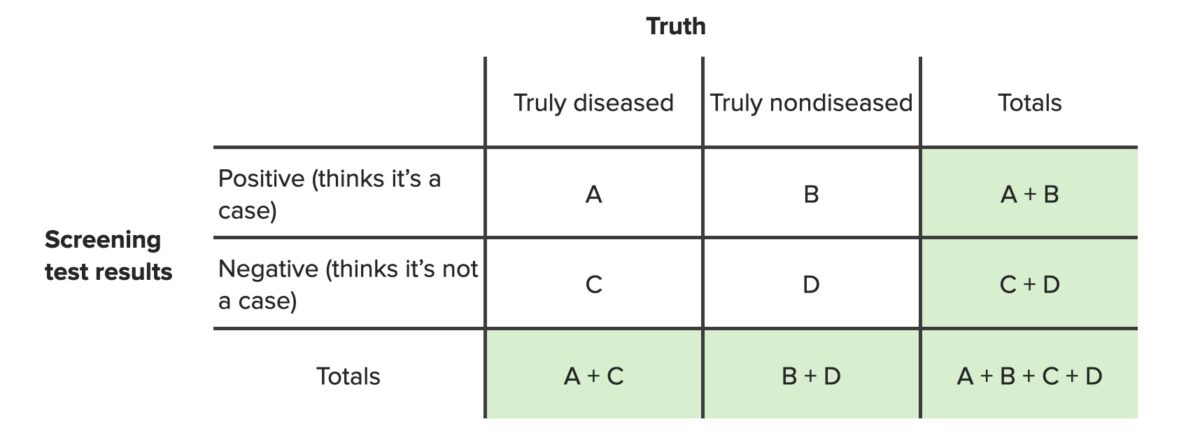
Tabela de contingência para testes de rastreio
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0Nesta tabela:
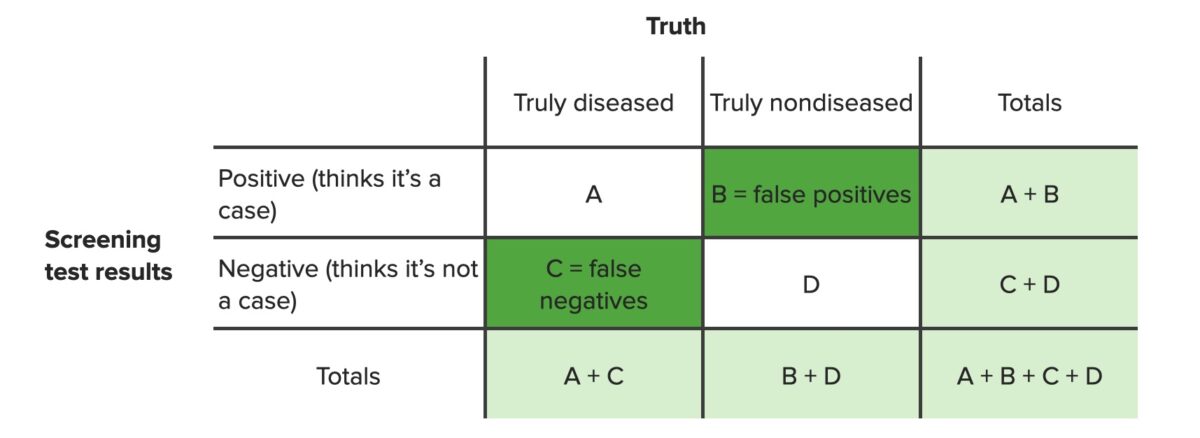
Tabela de contingência identificando falsos positivos (B) e falsos negativos (C)
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0Sensibilidade e especificidade são medidas utilizadas para avaliar o desempenho dos testes Testes Gonadal Hormones de rastreio e diagnóstico.
Definição:
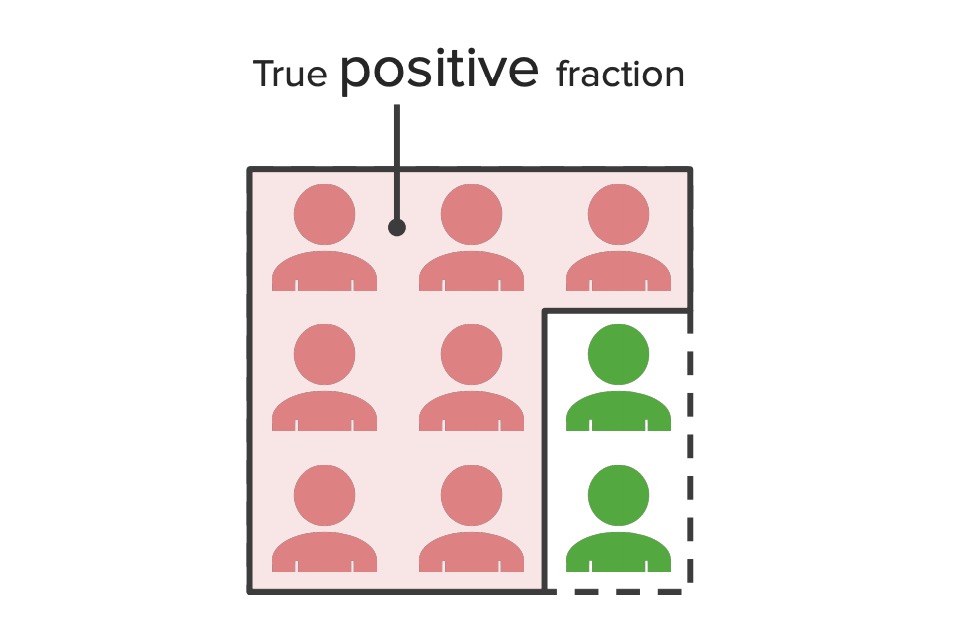
Fração positiva verdadeira:
Diagrama que ilustra o conceito de frações positivas verdadeiras – a proporção da população representada pela sensibilidade de um teste. Esta figura mostra que todos os pacientes testaram positivo; no entanto, as figuras verdes representam indivíduos que não tiveram a doença, mas cujo teste foi incorretamente positivo (falsos positivos). As figuras vermelhas representam os indivíduos que realmente tiveram a doença e também testaram positivo (verdadeiros positivos).
Cálculo:
Para calcular a sensibilidade, deve preencher-se uma tabela de contingência 2×2:

Tabela de contingência para testes de rastreio
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0A sensibilidade é a proporção de indivíduos que testam positivo no teste de rastreio e que têm a doença (VPs, encontrados na célula A) dividida por todos os indivíduos que estão realmente doentes, independentemente dos resultados do teste de rastreio (VPs e FNs, A + C). A sensibilidade é representada pela seguinte equação:
$$ Sensibilidade = \frac{A}{A + C} $$Exemplo: Avalia-se um novo teste de diagnóstico num grupo de pacientes: sabe-se que 100 pacientes têm a doença e que outros 100 pacientes de um grupo de controlo não têm a doença. Entre eles, 90 pacientes com a doença e 20 indivíduos do grupo controlo apresentam resultado positivo. Qual é a sensibilidade do novo teste?
Resposta: Neste caso, havia 100 pacientes que sabidamente tinham a doença. A sensibilidade é a proporção desses pacientes que foram identificados corretamente com base no teste positivo. A tabela de contingência completa-se da seguinte forma:
| Doentes | Grupo de controlo | Total | |
|---|---|---|---|
| Teste positivo | 90 | 20 | 110 |
| Teste negativo | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Importância da sensibilidade:
Definição:
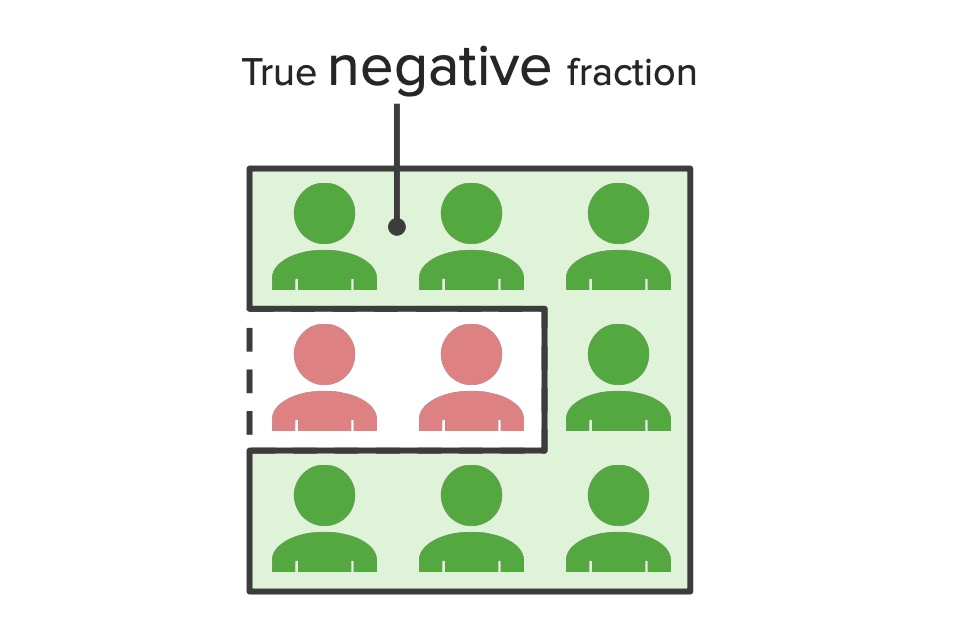
Fração negativa verdadeira:
Diagrama que ilustra o conceito de frações negativas verdadeiras – a proporção da população representada pela especificidade de um teste. Este diagrama mostra que todos os pacientes tiveram um resultado de teste negativo. As figuras vermelhas representam os indivíduos que realmente tiveram a doença, mas que testaram negativo (falsos negativos), enquanto as figuras verdes representam os indivíduos que não tiveram a doença e que testaram corretamente o negativo (verdadeiros negativos).
Cálculo:
A especificidade também é calculada usando uma tabela de contingência semelhante:

Tabela de contingência para testes de rastreio
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0A especificidade é a proporção de indivíduos que são verdadeiramente negativos e têm um teste de rastreio negativo (VNs, encontrado no quadrado D) dividida por todas os indivíduos que são realmente negativos, independentemente do resultado do teste de rastreio (VNs e FPs, B + D). A especificidade é representada pelas seguintes equações:
$$ Especificidade = \frac{D}{B + D}\ ou \ Especificidade = \frac{VN}{(FP + VN)} $$onde VN = verdadeiros negativos e FP FP An FP test result indicates that a person has the disease when they do not. Epidemiological Values of Diagnostic Tests = falsos positivos
Exemplo: Testa-se um novo teste de diagnóstico num grupo de pacientes: sabe-se que 100 pacientes têm a doença e que outros 100 pacientes de um grupo de controlo não têm a doença. Entre eles, 90 pacientes com a doença e 20 indivíduos do grupo de controlo apresentam um resultado positivo. Qual é a especificidade do novo teste?
Resposta: Neste caso, sabe-se que todos os pacientes do grupo controlo estão livres de doença. A especificidade é a proporção desses pacientes que foram identificados corretamente com base no teste negativo. A tabela de contingência completa-se da seguinte forma:
| Doentes | Grupo de controlo | Total | |
|---|---|---|---|
| Teste positivo | 90 | 20 | 110 |
| Teste negativo | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Importância da especificidade:
Os valores preditivos também são chamados “taxas de precisão”.
Definição:
O valor preditivo positivo é a percentagem de indivíduos com teste positivo que realmente tem a doença entre todas as pessoas com resultado positivo (A), independentemente de terem ou não a doença (A+B).
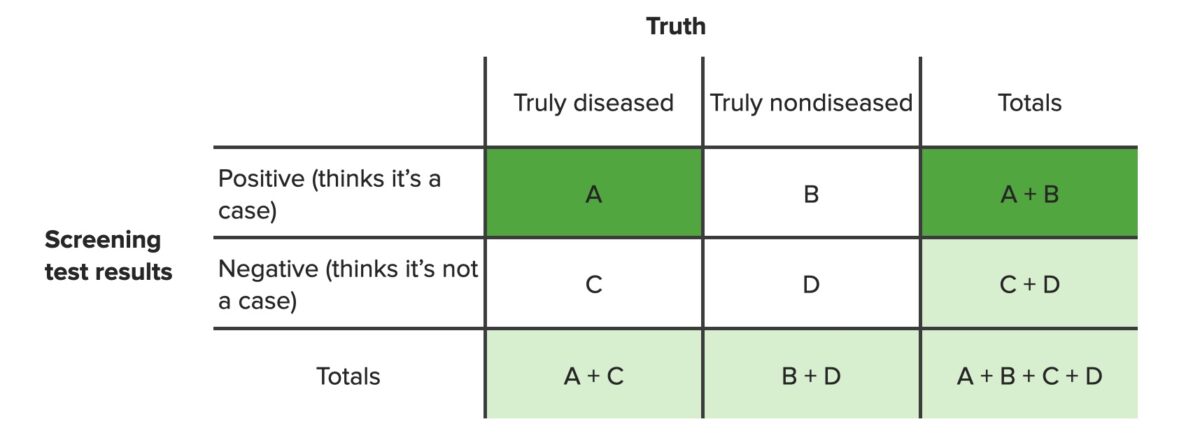
Tabela de contingência destacando os valores necessários para o cálculo do valor preditivo positivo
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0Cálculo:
O valor preditivo positivo é calculado usando a equação:
$$ Valor\ preditivo\ positivo = \frac{A}{A + B} $$em que A = verdadeiros positivos e B = falsos positivos
Exemplo: Testa-se um novo teste de diagnóstico num grupo de pacientes: sabe-se que 100 pacientes têm a doença e que outros 100 pacientes de um grupo de controlo não têm a doença. Entre eles, 90 pacientes com a doença e 20 indivíduos do grupo controlo apresentam resultado positivo. Qual é o valor preditivo positivo do novo teste?
Resposta: O valor preditivo positivo questiona a proporção de casos VP de entre todos os casos positivos (VP + FP FP An FP test result indicates that a person has the disease when they do not. Epidemiological Values of Diagnostic Tests). A tabela de contingência completa-se da seguinte forma:
| Doentes | Grupo de controlo | Total | |
|---|---|---|---|
| Teste positivo | 90 | 20 | 110 |
| Teste negativo | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Diferença entre valor preditivo positivo e sensibilidade:
Definição:
O VPN é a percentagem de indivíduos com resultado negativo no teste que estão realmente livres da doença (D), entre todos os indivíduos com resultado negativo (independentemente de terem ou não a doença, C + D).
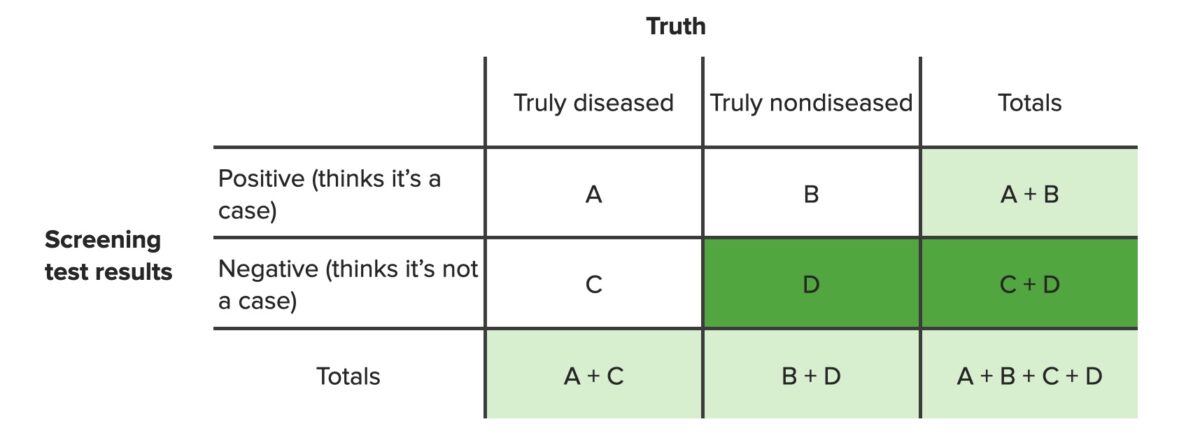
Tabela de contingência destacando os valores necessários para calcular o valor preditivo negativo
Imagem por Lecturio. Licença: CC BY-NC-SA 4.0Cálculo:
O VPN é calculado usando a seguinte equação:
$$ VPN = \frac{D}{C + D} $$em que D = verdadeiros negativos e C = falsos negativos
Exemplo: Testa-se um novo teste de diagnóstico num grupo de pacientes: sabe-se que 100 pacientes têm a doença e que outros 100 pacientes de um grupo de controlo não têm a doença. Entre eles, 90 pacientes com a doença e 20 indivíduos do grupo de controlo apresentam resultado positivo. Qual é o VPN do novo teste?
Resposta: O VPN questiona a proporção de casos VN de todos os casos negativos (VN + FN FN An FN test result indicates a person does not have the disease when, in fact, they do. Epidemiological Values of Diagnostic Tests). A tabela de contingência completa-se da seguinte forma:
| Doentes | Grupo de controlo | Total | |
|---|---|---|---|
| Teste positivo | 90 | 20 | 110 |
| Teste negativo | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Diferença entre VPN e especificidade:
Exemplo da gravidez:
Num estudo, 4.810 mulheres fazem um teste de gravidez de urina em casa. Todas foram submetidas a uma ecografia para confirmar se estão ou não realmente grávidas. Entre elas, 9 mulheres tiveram resultado positivo no teste de gravidez na urina e descobriram na ecografia que estavam grávidas; 1 mulher teve um resultado negativo no teste de gravidez na urina, mas na verdade estava grávida; 351 mulheres tiveram resultado positivo no teste de gravidez de urina e não estavam grávidas; 4.449 mulheres tiveram resultado negativo no teste de gravidez na urina e o resultado da ecografia confirmou que não estavam grávidas. (Nota: estes são dados de uma amostra e não representam valores reais.)
Neste exemplo, o teste de gravidez em casa é o teste de rastreio e “gravidez” é o estado de “doença”.
A tabela de contingência é a seguinte:
| Grávida | Não grávida | Total | |
|---|---|---|---|
| Teste positivo | 9 | 351 | 360 |
| Teste negativo | 1 | 4,449 | 4,450 |
| Total | 10 | 4,800 | 4,810 |
| Pergunta clínica | O que está a ser perguntado? | Equação | Resposta |
|---|---|---|---|
| Se a mulher está realmente grávida, qual é a probabilidade de o teste de gravidez na urina ser positivo? | Sensibilidade | = A / (A + C)
= 9 / (10) |
90% |
| Se uma mulher não está realmente grávida, qual é a probabilidade de o teste de gravidez na urina mostrar corretamente que ela não está grávida? | Especificidade | = B / (B + D)
= 4.449 / 4.800 |
92,7% |
| Se uma mulher testar positivo no teste de gravidez de urina, qual é a probabilidade de estar realmente grávida? | Valor Preditivo Positivo | = A / (A + B)
= 9/360 |
2,5% |
| Se uma mulher testar negativo no teste de gravidez de urina, qual é a probabilidade de realmente não estar grávida? | VPN | = D / (C + D)
= 4.449 / 4.450 |
99,9% |
Usando o mesmo exemplo de gravidez na secção acima, e sabendo que a sensibilidade foi de 90% e a especificidade de 92,7%, o LR+ e o LR‒ podem ser calculados da seguinte forma:
LR+ = 0,9 / (1 ‒ 0,927) = 12,3 = 1230%
LR‒ = (1 ‒ 0,9) / 0,927 = 0,11 = 11%
Interpretação: Há uma probabilidade 12 vezes maior de uma mulher com teste positivo estar realmente grávida. Um resultado de teste negativo reduz as chances de estar grávida em 89%.