A probabilidade é uma ferramenta matemática usada para estudar a aleatoriedade e fornecer previsões sobre a possibilidade de algo acontecer. Existem várias regras básicas de probabilidades que podem ser usadas para ajudar a determinar a probabilidade de vários eventos acontecerem juntos, separadamente ou sequencialmente. Este artigo aborda os fundamentos da probabilidade, que são importantes tanto na condução e na interpretação dos resultados de ensaios clínicos quanto na tomada de decisões clínicas para pacientes com base na probabilidade de resultados diferentes.
Última atualização: Jul 28, 2022
A probabilidade é uma ferramenta matemática usada para estudar a aleatoriedade e fornecer previsões sobre a possibilidade de algo acontecer.
Exemplo de probabilidade:
Se você jogar uma moeda equilibrada, a probabilidade teórica de cara em qualquer lance é de 50%.
Exemplo de resultados a curto prazo versus resultados a longo prazo:
Se você jogar uma moeda equilibrada, há 50% de chance de obter cara em qualquer lance. Se você lançar 10 caras seguidas, isso não aumenta a chance de obter cara no próximo lance (um resultado a curto prazo). A LGN significa que, num grande número de lançamentos de moedas, a frequência de obter caras será próxima de 50%.
A probabilidade de um evento (A) acontecer está entre 0 (certeza absoluta de que não ocorrerá) e 1 (certeza absoluta de sua ocorrência):
$$ 0\leq P(A)\leq 1 $$A soma de todas as probabilidades de todos os resultados possíveis num espaço amostral é 1:
$$ P(S) = 1 $$Fenómenos aleatórios são situações em que os resultados possíveis são conhecidos, mas o que acontecerá é desconhecido.
Alguns eventos têm apenas 2 resultados possíveis: o evento A ocorre ou o evento A não ocorre. O complemento do evento A é que o evento A não ocorre e é representado como A (ou AC). A probabilidade de A ocorrer é igual a 1 menos a probabilidade do próprio evento (A).
$$ P(A^{C}) = 1 – P(A) $$
Um diagrama de Venn que ilustra a regra do complemento:
A caixa cinzenta inteira representa o espaço amostral, que é igual a 1. O evento A representa uma parte da caixa e a não ocorrência do evento A representa a parte restante do espaço amostral. Da palestra “Introduction to Probability”
Exemplo: Você tem uma chance de 1 em 4 de tirar uma carta de paus de um baralho de cartas padrão. Qual é a probabilidade de você não tirar uma carta de paus?
Resposta: Neste exemplo, tirar uma carta de paus é o evento A e não tirar uma carta de paus é A. Se a chance de tirar uma carta de paus é 0,25, então A = 1 ‒ 0,25, que é 0,75.
Se 2 ou mais eventos não podem ocorrer simultaneamente, são chamados de eventos mutuamente exclusivos ou disjuntos. Embora não seja possível que os 2 eventos disjuntos ocorram simultaneamente, é possível que nenhum deles ocorra.
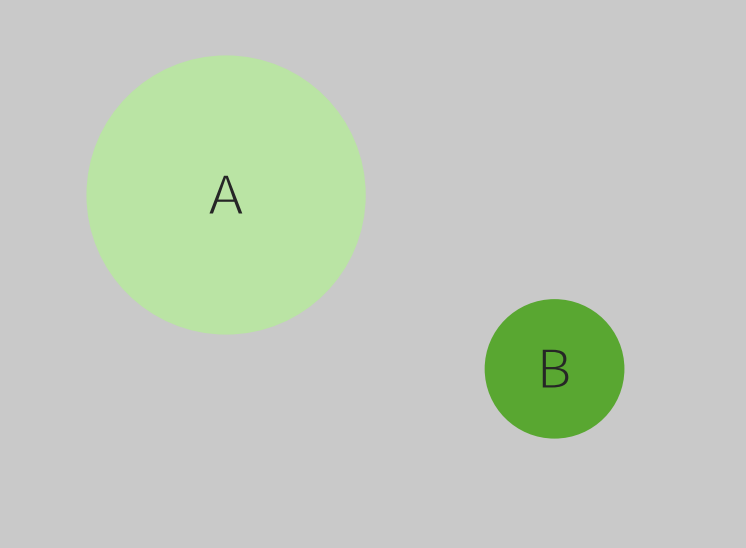
Um diagrama de Venn ilustrando a regra dos eventos mutuamente exclusivos:
A área da caixa representa todo o espaço amostral, que é igual a 1. O círculo A representa a probabilidade do evento A ocorrer e o círculo B representa a probabilidade do evento B ocorrer.
Os círculos não se sobrepõem, indicando que são mutuamente exclusivos e não podem ocorrer simultaneamente. É possível, no entanto, que nenhum dos eventos ocorra. Observe como eles não se sobrepõem.
Quando 2 eventos (A e B) são mutuamente exclusivos (ou disjuntos), a probabilidade de ocorrência de A ou B é a soma da probabilidade de cada evento.
$$ P(A\cup B) = P(A) + P(B) $$Esta regra pode ser aplicada a qualquer número de eventos disjuntos. Por exemplo, para encontrar a probabilidade de ocorrência de A, B ou C, você pode simplesmente adicionar P(A) + P(B) + P(C), supondo que todos os 3 sejam eventos completamente mutuamente exclusivos.
Exemplo 1:
Exemplo 2:
Os eventos são independentes quando a probabilidade de um não afeta a do outro (Nota: eventos mutuamente exclusivos não podem ser eventos independentes (Exemplo 2)). A probabilidade de 2 eventos independentes ocorrerem é igual ao produto das probabilidades dos eventos A e B.
$$ P(A\cap B) = P(A)P(B) $$Exemplo 1:
Exemplo 2: Eventos mutuamente exclusivos não podem ser independentes uns dos outros
A probabilidade de acontecer um evento (A), ou outro evento (B), ou ambos é dada pela equação:
$$ P(A\cup B) = P(A) + P(B) – P(A\cap B) $$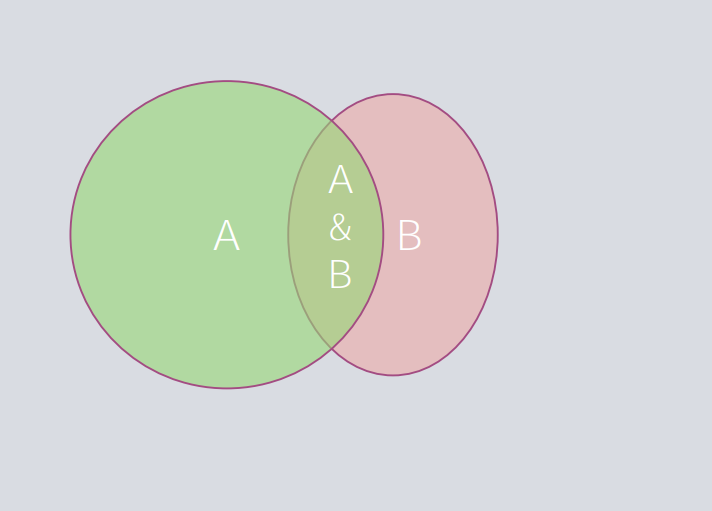
Um diagrama de Venn que ilustra a regra geral de adição de probabilidades:
A área de toda a caixa cinzenta representa todo o espaço amostral, que é igual a 1. Há um círculo que encapsula a probabilidade do evento A ocorrer (verde) e outro para o evento B (vermelho). A área onde eles se sobrepõem representa a probabilidade de ambos os eventos ocorrerem simultaneamente.
Portanto, se você simplesmente adicionasse a área do círculo verde à do círculo vermelho, a área sobreposta seria contada duas vezes. Visualmente, a probabilidade total de A, B ou ambos ocorrerem pode ser representada como P(A) + [P(B) ‒ P(A&B)].
Exemplo: Você tem uma pilha de dinheiro com 4 notas: $ 1, $ 5, $ 10 e $ 20. O evento A representa tirar uma nota ímpar; o evento B representa tirar uma nota entre $ 4 e $ 12. Qual é a probabilidade de acontecer A ou B?
Resposta: Observe que $5 está em ambos os eventos; portanto, não são mutuamente exclusivos ou disjuntos. Assim, não podemos simplesmente somar P(A) + P(B), pois teremos contado a probabilidade de ser tirada uma nota de $5 (P($5)) duas vezes. Devemos, portanto, subtrair P($5) para que seja contada apenas uma vez no final. Se as chances de tirar cada nota são as mesmas, então a probabilidade de tirar cada nota individual é de 1 em 4, ou 25%.
Então, para responder à nossa pergunta, primeiro podemos calcular P(A), que é igual a P($1) + P($5) = 0,25 + 0,25 = 0,5. Da mesma forma, P(B) = P($5) + P($10) = 0,25 + 0,25 = 0,5. Sabemos que P($5) por si só é 0,25. Então, no geral, 0,5 + 0,5 ‒ 0,25 = 0,75, o que representa 3 das 4 notas (as notas de $ 1, $ 5 e $ 10, que estão todas incluídas no evento A ou B).
USMLE™ is a joint program of the Federation of State Medical Boards (FSMB®) and National Board of Medical Examiners (NBME®). MCAT is a registered trademark of the Association of American Medical Colleges (AAMC). NCLEX®, NCLEX-RN®, and NCLEX-PN® are registered trademarks of the National Council of State Boards of Nursing, Inc (NCSBN®). None of the trademark holders are endorsed by nor affiliated with Lecturio.
Complementa o teu estudo da faculdade com o companheiro de estudo tudo-em-um da Lecturio, através de métodos de ensino baseados em evidência.
A Lecturio Medical complementa o teu estudo através de métodos de ensino baseados em evidência, vídeos de palestras, perguntas e muito mais – tudo combinado num só lugar e fácil de usar.
