Las pruebas diagnósticas son aspectos importantes para hacer un diagnóstico. Cierta información estadística sobre la precisión y validez de las pruebas en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum sí puede ayudar a convertir los LOS Neisseria datos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum información útil y aplicable. Algunos de los LOS Neisseria valores epidemiológicos más importantes de las pruebas de diagnóstico incluyen sensibilidad y especificidad, falsos positivos y falsos negativos, valores predictivos positivos y negativos, cocientes de probabilidad y probabilidades previas y posteriores a la prueba. Por ejemplo, una prueba con alta sensibilidad es útil como prueba de tamizaje, mientras que se requiere una alta especificidad para un diagnóstico preciso. Alternativamente, los LOS Neisseria valores predictivos positivos y negativos ayudan a determinar la probabilidad de enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el caso de ciertos resultados de una prueba.
Last updated: Jul 28, 2022
Contents
Las pruebas de tamizaje se utilizan para identificar a personas en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum las primeras etapas de una enfermedad y permitir una intervención temprana con el objetivo de reducir la morbilidad y la mortalidad.
Las pruebas de tamizaje no proporcionan un diagnóstico definitivo:
La utilidad de las pruebas de tamizaje requiere la evaluación de:
Las tablas de contingencia se utilizan comúnmente en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el análisis estadístico de múltiples variables. Para evaluar el valor epidemiológico de una prueba de tamizaje, se puede usar una tabla similar a la que se presenta a continuación para determinar las frecuencias relativas de individuos con diferentes combinaciones de resultados de la prueba de tamizaje (positivos o negativos) y el estado real de la enfermedad (realmente tienen o no tienen la enfermedad).
Es importante que la tabla esté configurada de manera estándar para que las fórmulas estándar sean aplicables. La tabla estándar se presenta a continuación (con los LOS Neisseria resultados de las pruebas de tamizaje a la izquierda, el estado real de la enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la parte superior y las respuestas “sí” antes de las respuestas “no”).
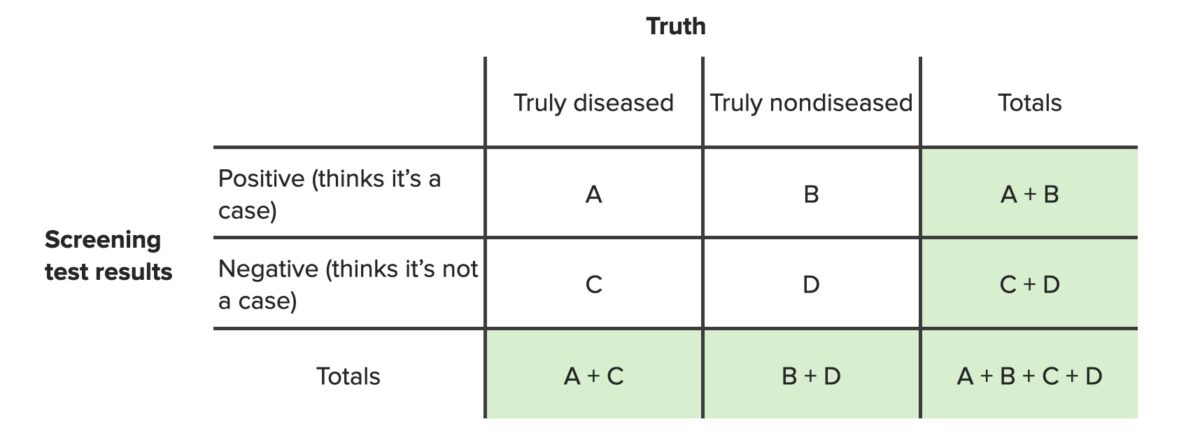
Tabla de contingencia para pruebas de tamizaje
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum esta tabla:
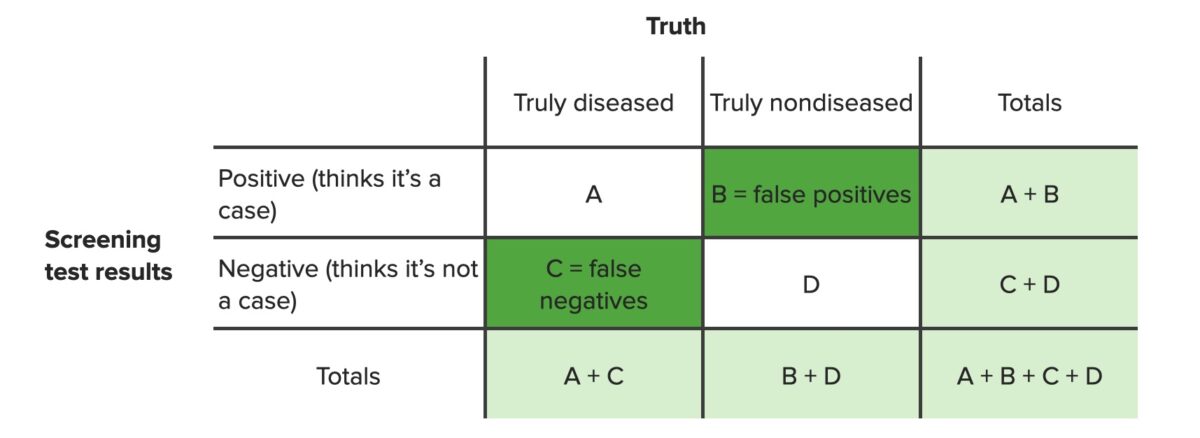
Tabla de contingencia identificando falsos positivos (B) y falsos negativos (C)
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0La sensibilidad y la especificidad son medidas utilizadas para evaluar el rendimiento de las pruebas de tamizaje y de diagnóstico.
Definición:
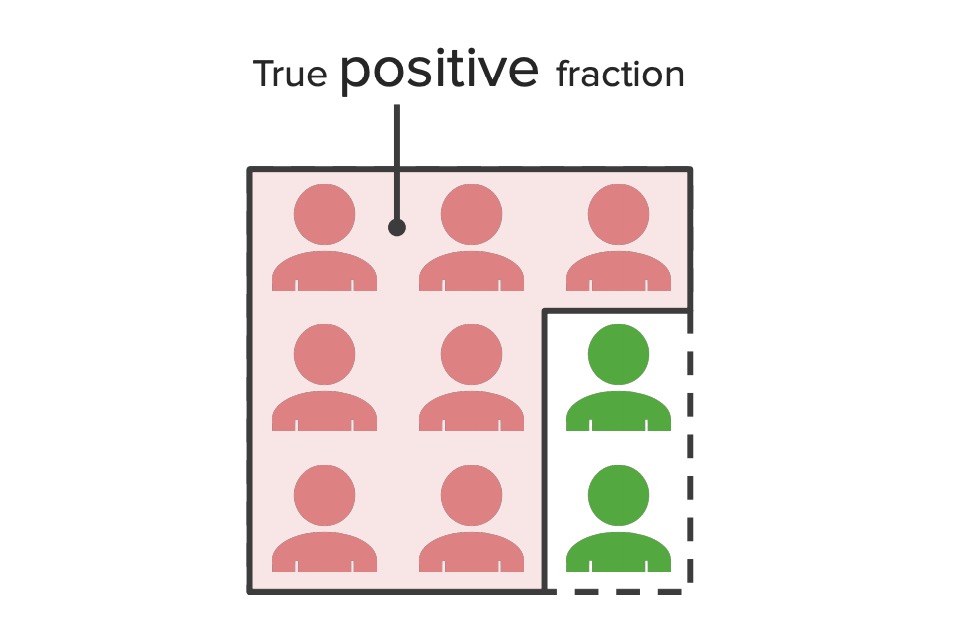
Fracción positiva verdadera:
Diagrama que ilustra el concepto de fracciones positivas verdaderas – la proporción de la población representada por la sensibilidad de una prueba. Esta figura muestra que todos los pacientes resultaron positivo; sin embargo, las figuras verdes representan individuos que no tenían la enfermedad, pero, incorrectamente, resultaron positivo (falsos positivos). Las figuras rojas representan a las personas que realmente tenían la enfermedad y también resultaron positivo (verdaderos positivos).
Cálculos:
Para calcular la sensibilidad, se debe configurar una tabla de contingencia de 2×2:
Tabla de contingencia para pruebas de tamizaje
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0La sensibilidad es la proporción de personas que resultan positivo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de tamizaje y tienen la enfermedad (verdaderos positivos, que se encuentra en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el cuadrado A) dividida entre todas las personas que están realmente enfermas, independientemente de los LOS Neisseria resultados de la prueba de tamizaje (verdaderos positivos y falsos negativos, A + C). La sensibilidad está representada por la siguiente ecuación:
$$ Sensibilidad = \frac{A}{A + C} $$Ejemplo: Se evalúa una nueva prueba de diagnóstico en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo de pacientes: se sabe que 100 pacientes tienen la enfermedad y otros 100 pacientes se sabe que están libres de la enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo control. Entre ellos, 90 pacientes con la enfermedad y 20 individuos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo control muestran un resultado positivo. ¿Cuál es la sensibilidad de la nueva prueba?
Respuesta: En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum este caso, había 100 pacientes que se sabía que tenían la enfermedad. La sensibilidad es la proporción de estos pacientes que fueron identificados correctamente en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum base a la prueba positiva. Configure una tabla de contingencia de la siguiente manera:
| Enfermos | Grupo control | Total | |
|---|---|---|---|
| Prueba positiva | 90 | 20 | 110 |
| Prueba negativa | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Importancia de la sensibilidad:
Definición:
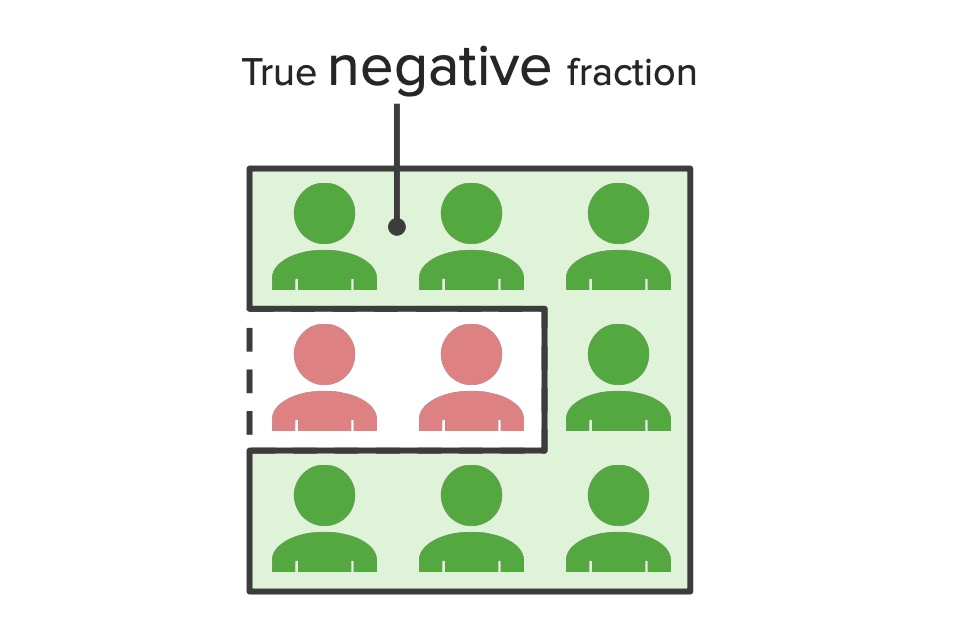
Fracción negativa verdadera:
Diagrama que ilustra el concepto de fracciones negativas verdaderas – la proporción de la población representada por la especificidad de una prueba. Este diagrama muestra que todos los pacientes recibieron un resultado de prueba negativo. Las cifras rojas representan personas que realmente tenían la enfermedad, pero resultaron negativo (falsos negativos), mientras que las figuras verdes representan personas que no tenían la enfermedad y, correctamente, resultaron negativo (verdaderos negativos).
Cálculo:
La especificidad también se calcula utilizando una tabla de contingencia similar:
Tabla de contingencia para pruebas de tamizaje
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0La especificidad es la proporción de personas que son realmente negativas y tienen una prueba de tamizaje negativa (verdaderos negativos, que se encuentra en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el cuadro D) dividida entre todas las personas que son realmente negativas, independientemente de los LOS Neisseria resultados de su prueba de tamizaje (verdaderos negativos y falsos positivos, B + D). La especificidad está representada por las siguientes ecuaciones:
$$ Especificidad = \frac{D}{B + D}\ o \ Especificidad = \frac{VN}{(FP + VN)} $$donde VN = verdaderos negativos y FP FP An FP test result indicates that a person has the disease when they do not. Epidemiological Values of Diagnostic Tests = falsos positivos
Ejemplo: Se prueba una nueva prueba de diagnóstico en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo de pacientes: se sabe que 100 pacientes tienen la enfermedad y se sabe que otros 100 pacientes están libres de la enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo control. Entre ellos, 90 pacientes con la enfermedad y 20 individuos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo control muestran un resultado positivo. ¿Cuál es la especificidad de la nueva prueba?
Respuesta: En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum este caso, se sabe que todos los LOS Neisseria pacientes del grupo control están libres de enfermedad. La especificidad es la proporción de estos pacientes que fueron identificados correctamente en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum base a la prueba negativa. Configure una tabla de contingencia de la siguiente manera:
| Enfermos | Grupo control | Total | |
|---|---|---|---|
| Prueba positiva | 90 | 20 | 110 |
| Prueba negativa | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Importancia de la especificidad:
Los LOS Neisseria valores predictivos también se denominan “índices de precisión”.
Definición:
El valor predictivo positivo es el porcentaje de personas con resultado positivo que realmente tienen la enfermedad entre todas las personas con resultado positivo (A), independientemente de que tengan o no la enfermedad (A+B).
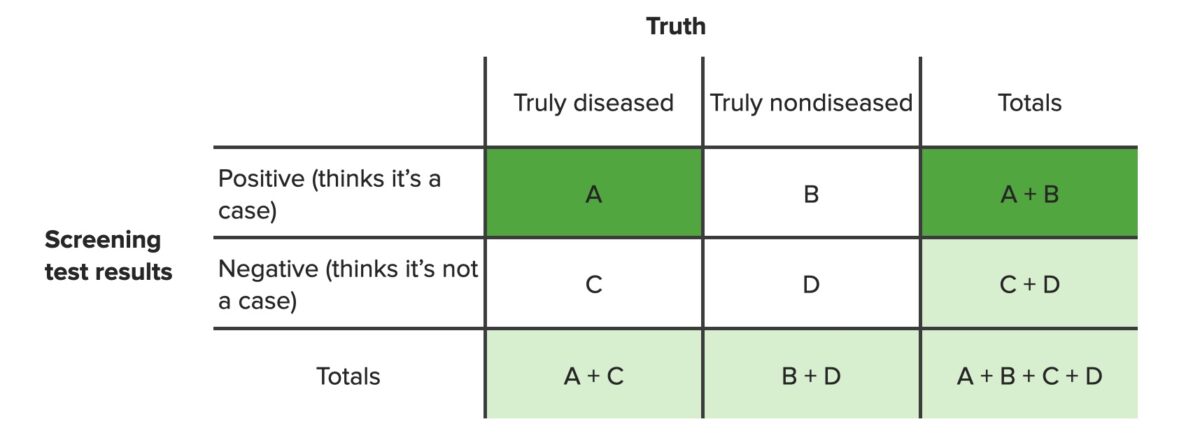
Tabla de contingencia que destaca los valores necesarios para el cálculo del valor predictivo positivo
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0Cálculo:
El valor predictivo positivo se calcula mediante la ecuación:
$$ Valor\ predictivo\ positivo = \frac{A}{A + B} $$donde A = verdaderos positivos y B = falsos positivos
Ejemplo: Se prueba una nueva prueba de diagnóstico en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo de pacientes: se sabe que 100 pacientes tienen la enfermedad y se sabe que otros 100 pacientes están libres de la enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo control. Entre ellos, 90 pacientes con la enfermedad y 20 individuos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo control muestran un resultado positivo. ¿Cuál es el valor predictivo positivo de la nueva prueba?
Respuesta: El valor predictivo positivo pregunta sobre la proporción de casos de verdaderos positivos de todos los LOS Neisseria casos positivos (verdaderos positivos + falsos positivos). Configure una tabla de contingencia de la siguiente manera:
| Enfermos | Grupo control | Total | |
|---|---|---|---|
| Prueba positiva | 90 | 20 | 110 |
| Prueba negativa | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Diferencia entre valor predictivo positivo y sensibilidad:
Definición:
El valor predictivo negativo es el porcentaje de personas con resultado negativo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba que realmente están libres de la enfermedad (D), entre todas las personas con resultado negativo (independientemente de que tengan o no la enfermedad, C + D).
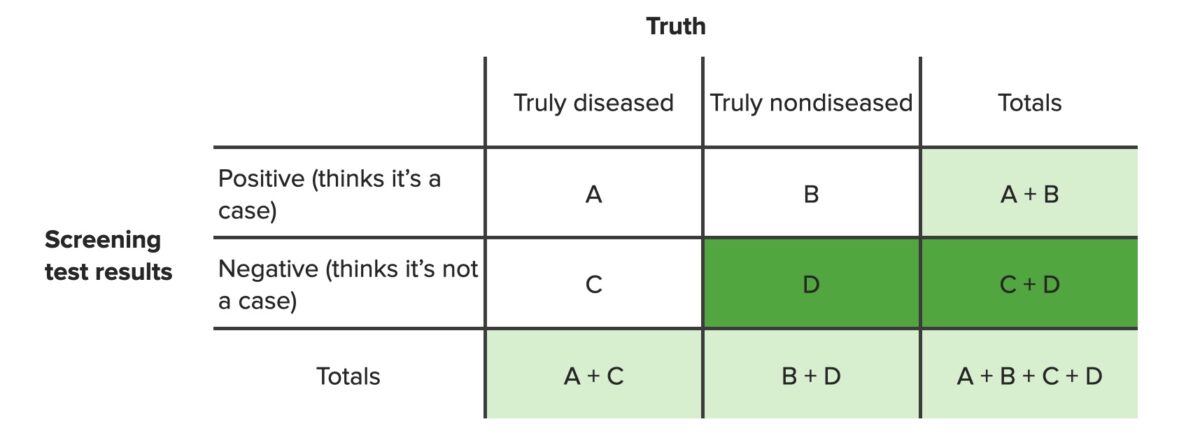
Tabla de contingencia que destaca los valores necesarios para calcular el valor predictivo negativo
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0Cálculo:
El valor predictivo negativo se calcula utilizando la siguiente ecuación:
$$ Valor\ predictivo\ negativo = \frac{D}{C + D} $$donde D = verdaderos negativos y C = falsos negativos
Ejemplo: Se prueba una nueva prueba de diagnóstico en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo de pacientes: se sabe que 100 pacientes tienen la enfermedad y se sabe que otros 100 pacientes están libres de la enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo control. Entre ellos, 90 pacientes con la enfermedad y 20 individuos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo control muestran un resultado positivo. ¿Cuál es el valor predictivo negativo de la nueva prueba?
Respuesta: El valor predictivo negativo pregunta sobre la proporción de casos verdaderos negativos de todos los LOS Neisseria casos negativos (verdaderos negativos + falsos negativos). Configure una tabla de contingencia de la siguiente manera:
| Enfermos | Grupo control | Total | |
|---|---|---|---|
| Prueba positiva | 90 | 20 | 110 |
| Prueba negativa | 10 | 80 | 90 |
| Total | 100 | 100 | 200 |
Diferencia entre valor predictivo negativo y especificidad:
Ejemplo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum embarazo:
En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un estudio, 4810 mujeres se hicieron una prueba de embarazo casera en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina. A todas ellas se les realiza un ultrasonido para confirmar si realmente están embarazadas o no. Entre ellas, 9 mujeres tienen un resultado positivo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina y en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum realidad se descubre que están embarazadas en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un ultrasonido; 1 mujer tiene un resultado negativo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina, pero en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum realidad está embarazada; 351 mujeres tienen resultados positivos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina y se encuentra que no están embarazadas; 4449 mujeres tienen resultados negativos en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina y los LOS Neisseria resultados del ultrasonido confirman que no están embarazadas. (Nota: estos son datos de muestra y no representan valores reales).
En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum este ejemplo, la prueba de embarazo casera es la prueba de tamizaje y “embarazo” es el estado de “enfermedad”.
La tabla de contingencia es la siguiente:
| Embarazada | No embarazada | Total | |
|---|---|---|---|
| Prueba positiva | 9 | 351 | 360 |
| Prueba negativa | 1 | 4 449 | 4 450 |
| Total | 10 | 4 800 | 4 810 |
| Pregunta clínica | ¿Qué se está preguntando? | Ecuación | Respuesta |
|---|---|---|---|
| Si la mujer está realmente embarazada, ¿cuál es la probabilidad de que la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina sea positiva? | Sensibilidad | = A / (A + C)
= 9 / (10) |
90% |
| Si una mujer no está realmente embarazada, ¿cuál es la probabilidad de que la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina muestre correctamente que no está embarazada? | Especificidad | = B / (B + D)
= 4 449 / 4 800 |
92,7% |
| Si una mujer da positivo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina, ¿cuál es la probabilidad de que realmente esté embarazada? | Valor predictivo positivo | = A / (A + B)
= 9 / 360 |
2,5% |
| Si una mujer da negativo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum orina, ¿cuál es la probabilidad de que realmente no esté embarazada? | Valor predictivo negativo | = D / (C + D)
= 4 449 / 4 450 |
99,9% |
Usando el mismo ejemplo de embarazo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la sección anterior, y sabiendo que la sensibilidad fue del 90% y la especificidad del 92,7%, el cociente de probabilidad + y el cociente de probabilidad ‒ se pueden calcular de la siguiente manera:
Cociente de probabilidad + = 0,9 / (1 ‒ 0,927) = 12,3 = 1,230%
Cociente de probabilidad ‒ = (1 ‒ 0,9) / 0,927 = 0,11 = 11%
Interpretación: Hay una probabilidad 12 veces mayor de que una mujer que da positivo esté realmente embarazada. Un resultado negativo en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la prueba reduce las probabilidades de estar embarazada en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un 89%.
USMLE™ es un programa conjunto de la Federation of State Medical Boards (FSMB®) y la National Board of Medical Examiners (NBME®). MCAT es una marca registrada de la Association of American Medical Colleges (AAMC). NCLEX®, NCLEX-RN® y NCLEX-PN® son marcas registradas del National Council of State Boards of Nursing, Inc (NCSBN®). Ninguno de los titulares de las marcas registradas está avalado ni afiliado a Lecturio.
Regístrate ahora y obtén acceso gratuito a Lecturio con páginas de concepto, videos médicos y cuestionarios para tu educación médica.