Domina Conceptos Médicos

Estudia para la escuela de medicina y tus examenes con Lecturio.

USMLE® Step 1    |    USMLE® Step 2    |    Exámenes del NBME®   |    ENARM    

Crea tu cuenta gratuita
Continue Learning
Biblioteca de Conceptos de Lecturio
Pruebas Estadísticas y Representación de Datos

Pruebas Estadísticas y Representación de Datos

Uno de los principales objetivos de la investigación y los estudios médicos es aprender qué asociaciones o resultados no son producto del azar. Según el diseño del estudio y los datos que proporciona, se puede aceptar o rechazar una hipótesis, lo que permite determinar la correlación. Las pruebas estadísticas son herramientas utilizadas por los investigadores para obtener información y significado de conjuntos de datos variables. Estas pruebas se presentan en varias formas, incluyendo, por ejemplo, las pruebas de chi-cuadrado y exacta de Fisher, y se eligen en función de las necesidades de los investigadores y de las características de las variables analizadas. Los resultados del estudio pueden considerarse estadísticamente significativos en función de los valores p calculados y los niveles de significancia predeterminados (conocidos como nivel α). Los intervalos de confianza son otra forma de expresar la importancia de un resultado estadístico sin utilizar un valor p.

Última actualización: Ago 1, 2022

Responsabilidad editorial: Stanley Oiseth, Lindsay Jones, Evelin Maza

Contenido

Introducción

La comprobación de hipótesis se utiliza para evaluar la admisibilidad de una hipótesis mediante el análisis de los datos del estudio.

Por ejemplo, una empresa crea un nuevo medicamento X destinado a tratar la hipertensión. La empresa quiere saber si el medicamento X funciona realmente para reducir la presión arterial, por lo que tiene que hacer comprobación de hipótesis.

Pasos para comprobar una hipótesis:

  1. Formule la hipótesis.
  2. Elija la prueba estadística que va a utilizar.
  3. Establezca el nivel de significancia.
  4. Calcule las pruebas estadísticas a partir de sus datos utilizando la prueba adecuada/elegida.
  5. Conclusiones:
    • Se decide rechazar o no rechazar la hipótesis nula del paso 1.
    • Esta decisión se basa en los niveles de significancia predeterminados en el paso 3.

Formulación de una Hipótesis

Una hipótesis es una respuesta preliminar a una pregunta de investigación (i.e., una “suposición” sobre cuáles serán los resultados). Hay 2 tipos de hipótesis: la hipótesis nula y la hipótesis alternativa.

Hipótesis nula

  • La hipótesis nula (H0) afirma que no hay diferencias entre las poblaciones que se estudian (o dicho de otra forma, que no hay relación entre las variables que se prueban).
  • Escrita como una fórmula, H0: µ1 = µ2, donde µ representa las medias (o promedios) de los grupos 1 y 2, respectivamente
  • Ejemplo: El medicamento X fue creado para reducir la presión arterial. Se diseña un experimento para comprobar si el medicamento X reduce realmente la presión arterial. El medicamento X se administra a 1 grupo, mientras que un 2do grupo recibe un placebo. La hipótesis nula sería que el medicamento X no tiene ningún efecto sobre la presión arterial y que ambos grupos tendrán la misma media de presión arterial al final del periodo de estudio.

Hipótesis alternativa

  • La hipótesis alternativa (H1) afirma que existe una diferencia entre las poblaciones estudiadas.
  • Escrito como una fórmula, H1: µ1≠ µ2
  • Ejemplo: en el experimento descrito anteriormente, la hipótesis alternativa es que el medicamento X reduce la presión arterial, y que los pacientes del grupo de estudio que reciben el medicamento X tendrán una presión arterial más baja que los pacientes del grupo de placebo al final del periodo de estudio.
  • H1 es una afirmación que los investigadores consideran cierta.

¿Qué es lo que realmente prueba el estudio?

  • Las pruebas de hipótesis sobre muestras nunca pueden verificar una hipótesis con certeza y solo pueden decir que una hipótesis tiene una cierta probabilidad de ser verdadera o falsa.
  • Un estudio de investigación con hipótesis rechazará o no rechazará la hipótesis nula.

Ejemplos

Ejemplo 1: rechazar la hipótesis nula

En el ejemplo anterior, si los resultados del ensayo muestran que el medicamento X reduce significativamente la presión arterial (es decir, hay suficientes pruebas estadísticas que lo apoyan), se rechaza la hipótesis nula (que postula que no hay diferencias entre los grupos) con una probabilidad determinada. Obsérvese que estos resultados no pueden confirmar la hipótesis alternativa, sino que solo la apoyan con una probabilidad dada, determinada por la distribución del muestreo en la población estudiada.

Ejemplo 2: no rechazar la hipótesis nula

En el ejemplo anterior, si los resultados del ensayo muestran que el medicamento X no redujo significativamente la presión arterial, el estudio no rechazó la hipótesis nula. Una vez más, hay que tener en cuenta que los resultados no pueden confirmar la hipótesis nula, sino que solo la apoyan con una probabilidad dada, determinada por la distribución del muestreo en la población estudiada

Tipos de errores y potencia

  • Error de tipo I:
    • La hipótesis nula es verdadera, pero se rechaza.
    • La probabilidad de cometer un error de tipo I se representa como α.
  • Error de tipo II:
    • La hipótesis nula es falsa, pero se acepta/no se rechaza.
    • La probabilidad de cometer un error de tipo II se representa como β.
  • Potencia:
    • La probabilidad de que una prueba rechace una hipótesis nula falsa correctamente
    • Potencia = 1 – β
    • La potencia depende de:
      • Tamaño de la muestra (e.g., mayor tamaño de la muestra → ↑ potencia)
      • Tamaño del efecto esperado (e.g., un efecto esperado más alto/más grande → ↑ potencia)
Types of errors

Tipos de errores

Imagen por Lecturio.

Videos relevantes

2:03
Null Hypothesis – Statistics Basics
5:11
Type I and Type II Errors – Data

Determinación de la Significancia Estadística

La significancia estadística es la idea de que es muy poco probable que todos los resultados de las pruebas se produzcan simplemente por azar. Para determinar la significancia estadística, es necesario establecer un valor α y calcular un valor p.

Valores p

Se puede crear un gráfico en el que los posibles resultados del estudio se representen en el eje de las abscisas (x) y la probabilidad de observar cada resultado se represente en el eje de las ordenadas (y). El área bajo la curva representa el valor p.

  • El valor p es la probabilidad de obtener un resultado determinado, suponiendo que la hipótesis nula sea cierta.
    • En otras palabras, el valor p es la probabilidad de que se obtenga este resultado si no hubiera ninguna relación entre las variables y que los resultados se produjeran simplemente por azar.
    • Como toda probabilidad, el valor p está entre 0 y 1.
  • Valores p más altos (áreas bajo la curva más grandes):
    • Indican una mayor probabilidad de que la hipótesis nula sea cierta
    • Sugieren que no hay relación entre las variables
    • Ejemplo: en el ejemplo anterior, un valor p de 0,6 significaría que es poco probable que el medicamento X se asocie con una disminución de la presión arterial.
  • Valores p más bajos (áreas bajo la curva más pequeñas):
    • Indican una baja probabilidad de que la hipótesis nula sea cierta
    • Sugiere que es poco probable que una correlación observada entre las variables se deba simplemente al azar y que probablemente exista una relación verdadera
    • Ejemplo: en el ejemplo anterior, un valor p de 0,02 sugiere que el medicamento X se asocia a una disminución de la presión arterial.
  • Si el valor p es inferior al nivel de significancia predeterminado (nivel α), puede rechazar la hipótesis nula, porque es probable que exista una relación real entre las variables.
  • Cuanto más bajo sea el valor p, más seguro se estará de que la relación entre las variables es cierta (y no se debe al azar).

Mnemotecnia:

“Si la p es baja, la (hipótesis) nula no encaja”.

A graphical representation of the p-value and α-levels

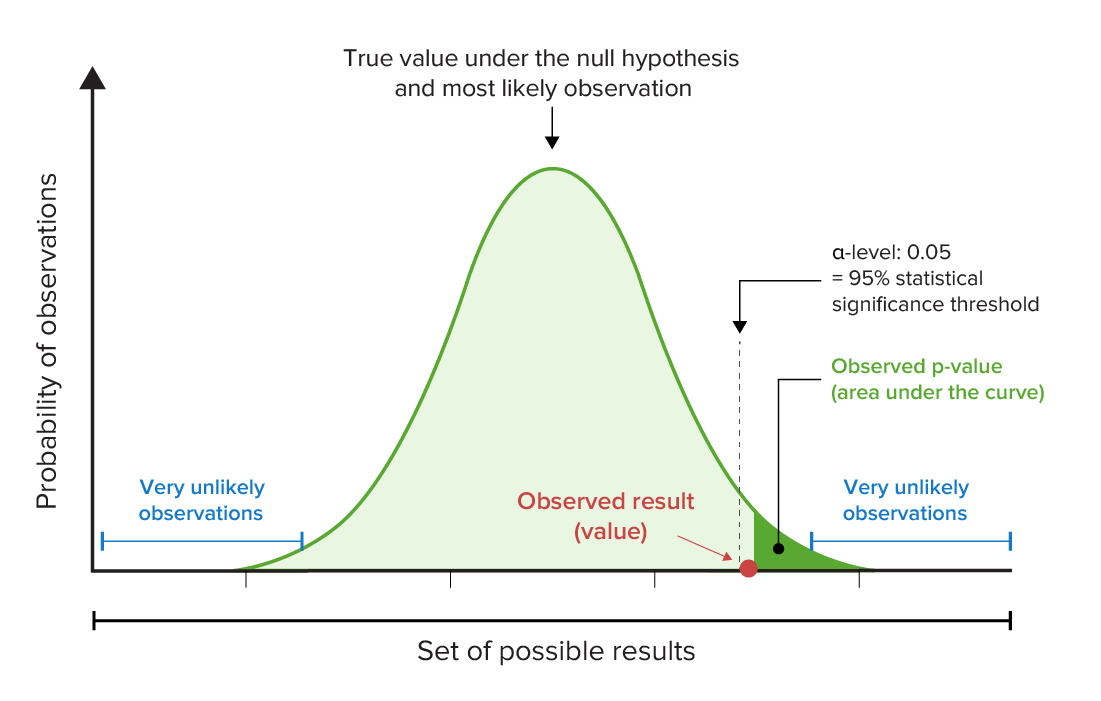
Representación gráfica del valor p y de los niveles α:
Observe, en este ejemplo, que el valor p observado es inferior al nivel de significancia estadística predeterminado (en este caso, el 95%). Esto significa que hay que rechazar la hipótesis nula porque el resultado observado sería muy improbable si la hipótesis nula (que no existe ninguna relación entre las variables) fuera cierta.

Imagen por Lecturio.

Nivel α

  • El nivel α es un valor p que representa un “nivel de significancia” determinado arbitrariamente.
  • El nivel α debe elegirse antes de realizar un estudio.
  • Por convención, el nivel α suele fijarse en 0,05 o 0,01.
  • El nivel α es el riesgo que se está dispuesto a asumir de tomar una decisión equivocada, en la que se rechace incorrectamente la hipótesis nula (cuando en realidad es verdadera).
  • Ejemplo:
    • Un nivel α de 0,05 significa que se concluirá que existe una relación entre las variables si el valor p es < 0,05.
    • Esto significa que se está dispuesto a aceptar hasta un 5% de probabilidad de cometer un error de tipo 1.
  • En el ejemplo del medicamento X-presión arterial, si el valor p fuera 0,03, se concluiría que:
    • El medicamento X se asocia a una disminución de la presión arterial → se trata de un rechazo de la hipótesis nula
    • Hay un 3% de probabilidad de que haya cometido un error de tipo 1: que la hipótesis nula fuera de hecho cierta y el medicamento X no esté realmente asociado a una menor presión arterial.

Intervalos de confianza

  • Un intervalo de confianza es la probabilidad de que el resultado caiga entre un rango definido de valores.
    • Los intervalos de confianza miden el grado de incertidumbre en el muestreo.
    • El intervalo de confianza es el rango de medias que se obtendría de un muestreo repetido de la misma población una y otra vez.
    • Los intervalos de confianza se calculan utilizando el tamaño de la muestra, la media de la muestra y la desviación estándar (se suelen utilizar calculadoras y tablas estándar en línea).
  • El nivel de confianza es la probabilidad de que el resultado verdadero se encuentre contenido dentro del intervalo de confianza
    • Lo más habitual es utilizar un nivel de confianza del 95% (aunque el nivel de confianza suele oscilar entre el 90% y el 99%)
    • Un intervalo de confianza del 95% es un rango de valores que contiene en un 95% de seguridad la verdadera media de la población.
    • Al igual que el nivel α, el nivel de confianza del intervalo se elige antes de probar los datos.
    • Cuanto mayor sea la confianza necesaria, mayor será el intervalo.
  • Ejemplo: los investigadores quieren determinar la altura media de una población de 1000 hombres. Se miden las alturas en una muestra aleatoria de 50 de estos hombres.
    • Se encuentra una altura media de 70 pulgadas.
    • Se calcula que el intervalo de confianza del 95% y está entre 68 y 72 pulgadas.
    • Esto significa que si los investigadores toman 100 muestras aleatorias de esa misma población, el 95% de las veces la media se situará entre 68 y 72 pulgadas. (No significa que el 95% de los datos de esa muestra estén entre 68 y 72 pulgadas).
    • Si se desea un mayor nivel de confianza, el rango se ampliará; por ejemplo, un intervalo de confianza del 99% puede dar lugar a un intervalo de confianza de 66 a 74 pulgadas.
90% confidence interval on a standard normal curve

Un intervalo de confianza del 90% en una curva normal estándar

Imagen por Lecturio.

Consideraciones en la comprobación de hipótesis

  • No base su hipótesis en lo que ve en los datos.
  • No haga de su H0 lo que quiere demostrar que es cierto.
  • Compruebe las condiciones.
  • No acepte la H0, sino que no la rechace.
  • No confunda la significancia clínica con la significancia estadística (e.g., con un tamaño de muestra suficientemente grande, puede encontrar que el medicamento X reduce la presión arterial sistólica en 2 mm Hg. Aunque esto sea estadísticamente significativo, ¿es clínicamente significativo para su paciente?)
  • Si no se rechaza la H0, no hay que suponer que un mayor tamaño de la muestra conducirá al rechazo.
  • Asegúrese de pensar si es razonable suponer que los eventos son independientes.
  • No interprete los valores p como la probabilidad de que la H0 sea verdadera.
  • Incluso una prueba realizada a la perfección puede ser errónea.

Videos relevantes

2:56
p-Value – Statistics Basics
2:20
Confidence Intervals – Statistics Basics
16:43
Testing Hypotheses about Proportions
14:04
More about Hypothesis Tests

Pruebas Estadísticas

Elegir la prueba adecuada

La elección de la prueba se basa en:

  • Los tipos de variables que está probando (tanto la “exposición” como el “resultado” de la prueba)
    • Cuantitativas: continuas (edad, peso, altura) o discretas (número de pacientes)
    • Categóricas: ordinales (clasificaciones; e.g., notas, talla de ropa), nominales (grupos con nombres; e.g., estado civil) o binarias (datos con solo una respuesta “sí/no”; e.g., vivo o muerto)
  • Si sus datos cumplen o no ciertos criterios conocidos como supuestos; los supuestos más comunes son:
    • Los datos son independientes unos de otros.
    • La varianza dentro de un mismo grupo es similar entre todos los grupos.
    • Los datos siguen una distribución normal (curva de campana).

Siempre hay que cuestionar la razonabilidad del modelo. Si el modelo es erróneo, también lo es todo lo demás.

Tenga cuidado con las variables que no son realmente independientes.

Variables continuas y categóricas

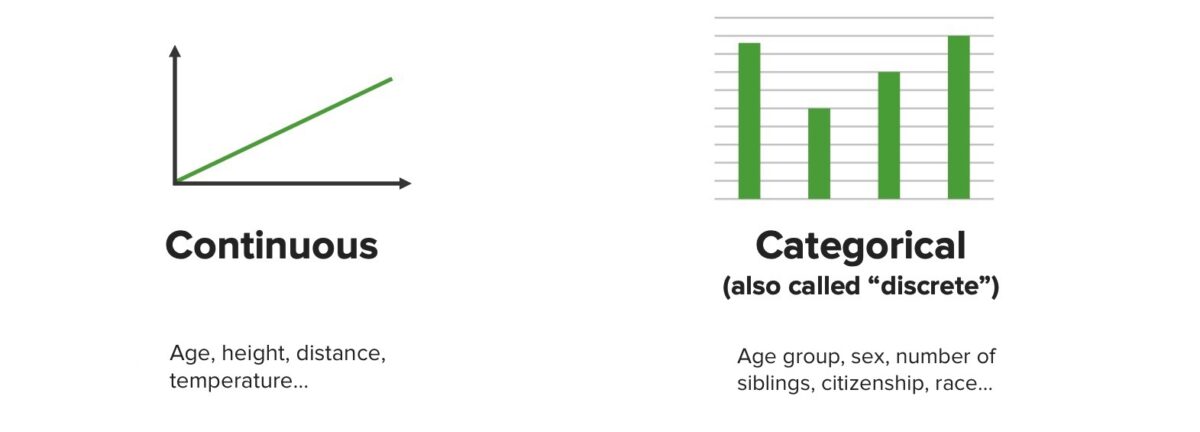
Representaciones gráficas de datos continuos y categóricos

Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0

Tipos de pruebas

Las 3 categorías principales de pruebas estadísticas son:

  1. Pruebas de regresión: evalúan las relaciones causa-efecto
  2. Pruebas de comparación: comparan las medias de diferentes grupos (requieren datos de resultados cuantitativos)
  3. Pruebas de correlación: buscan asociaciones entre diferentes variables
Tabla: Tipos de pruebas estadísticas
Nombre de la prueba Qué es lo que se comprueba en la prueba Tipos de variables/datos Ejemplo
Pruebas de regresión
Regresión lineal simple Cómo afecta un cambio en la variable de predicción/entrada a la variable de resultado
  • Predictor: continuo
  • Resultado: continuo
 ¿Cómo afecta el peso (predictor) a la esperanza de vida (resultado)?
Regresión lineal múltiple Cómo los cambios en las combinaciones de ≥ 2 variables predictoras pueden predecir los cambios en el resultado
  • Predictor: continuo
  • Resultado: continuo
 ¿Cómo afectan el peso y el nivel socioeconómico (predictores) a la esperanza de vida (resultado)?
Regresión logística Cómo ≥ 1 variables predictoras pueden afectar a un resultado binario
  • Predictor: continuo
  • Resultado: binario
 ¿Cuál es el efecto del peso (predictor) sobre la supervivencia (resultado binario: vivo o muerto)?
Pruebas de comparación
Prueba t pareada Compara las medias de 2 grupos de la misma población
  • Predictor: categórico
  • Resultado: cuantitativo
 Comparar el peso de los bebés (resultado) antes y después de la alimentación (predictor).
Prueba t independiente Compara las medias de 2 grupos de poblaciones diferentes
  • Predictor: categórico
  • Resultado: cuantitativo
 ¿Cuál es la diferencia de altura media (resultado) entre 2 equipos de baloncesto diferentes (predictor)?
Análisis de la varianza Compara las medias de > 2 grupos
  • Predictor: categórico
  • Resultado: cuantitativo
 ¿Cuál es la diferencia en los niveles de glucosa en sangre (resultado) 1, 2 y 3 horas después de una comida (predictores)?
Pruebas de correlación
Prueba chi-cuadrado Prueba la fuerza de la asociación entre 2 variables categóricas con un tamaño de muestra mayor
  • Variable 1: categórica
  • Variable 2: categórica
 Comparar si la aceptación en la facultad de medicina (variable 1) es más probable si el solicitante ha nacido en el Reino Unido (variable 2).
Prueba exacta de Fisher Prueba la fuerza de la asociación entre 2 variables categóricas con un tamaño de muestra menor
  • Variable 1: categórica
  • Variable 2: categórica
 Igual que el chi-cuadrado, pero con tamaños de muestra más pequeños
Prueba r de Pearson Prueba la fuerza de la asociación entre 2 variables continuas
  • Variable 1: continua
  • Variable 2: continua
 Comparar cómo el nivel de HbA1c en plasma (variable 1) está relacionado con los niveles de triglicéridos en plasma (variable 2) en pacientes diabéticos.

Prueba de chi-cuadrado (χ2)

Las pruebas de chi-cuadrado se utilizan habitualmente para analizar datos categóricos y determinar si 2 variables categóricas están relacionadas.

  • Qué pueden evaluar las pruebas de chi-cuadrado:
    • Si existe o no una asociación estadísticamente significativa entre 2 variables
    • Datos analizados: suelen ser datos categóricos “contados”, lo que significa que tiene un número de categorías nombradas, y sus datos son los valores contados para cada categoría.
    • Más preciso en muestras grandes que la prueba exacta de Fisher
  • Lo que las pruebas de chi-cuadrado no pueden evaluar:
    • La fuerza de esa asociación
    • Si la relación es causal

Para realizar una prueba de chi-cuadrado, se necesitan 2 datos: los grados de libertad (número de categorías menos 1) y el nivel α (que elige el investigador y suele fijarse en 0,05). Además, los datos deben organizarse en una tabla.

Ejemplo: si se quiere ver si los malabaristas tienen más probabilidades de nacer durante una estación determinada, los datos podrían registrarse en la siguiente tabla:

Categoría (i): temporada de nacimiento Frecuencia observada de malabaristas en cada estación de nacimiento
Primavera 66
Verano 82
Otoño 74
Invierno 78
Número total de malabaristas en la muestra: 300

Para empezar, hay que determinar las frecuencias esperadas para cada celda de la tabla anterior utilizando la ecuación:

$$ Frecuencia\ esperada = np_{0i} $$

donde n = el tamaño de la muestra y p0i es la proporción hipotética en cada categoría i.

En el ejemplo anterior, n = 300 y p0i es ¼, por lo que la frecuencia de celdas esperada es de 300 * 0,25 = 75 en cada celda.

La comprobación estadística se calcula entonces mediante la fórmula estándar de chi-cuadrado:

$$ \chi ^{2} = \sum _{all\ cells} \frac{(observada-esperada)^{2}}{esperada} $$

donde 𝝌2 es la prueba estadística que se calcula. para cada “celda” o categoría, la frecuencia esperada se resta de la frecuencia observada; este valor se eleva al cuadrado y luego se divide por la frecuencia esperada. Una vez calculada esta cifra para cada categoría, se suman los números.

Ejemplo de cálculo de 𝝌2: utilizando el ejemplo anterior, la frecuencia esperada en cada celda es 75, por lo que el 𝝌2 puede calcularse como sigue:

Categoría (i): temporada de nacimiento Frecuencia observada de malabaristas con cada estación de nacimiento (Observado – esperado)2/esperado
Primavera 66 (66 ‒ 75)2 / 75 = 1,08
Verano 82 (82 ‒ 75)2 / 75 = 0,653
Otoño 74 (74 ‒ 75)2 / 75 = 0,013
Invierno 78 (78 ‒ 75)2 / 75 = 0,12

𝝌2= 1,08 + 0,653 + 0,013 + 0,12 = 1,866

Determinar si la prueba estadística es estadísticamente significativa o no:

Para determinar si esta prueba estadística es estadísticamente significativa, se utiliza la tabla de chi-cuadrado para obtener el número crítico de chi-cuadrado.

  • La tabla tiene los grados de libertad (número de categorías menos 1) en el eje Y y el nivel α en el eje X.
  • Utilizando los grados de libertad y el nivel α del estudio, se encuentra el número crítico en el gráfico (véase el gráfico de ejemplo a continuación).
  • El número crítico se utiliza para determinar la significancia estadística comparándolo con el resultado calculado de la prueba estadística.
    • Si el resultado calculado de la prueba estadística > valor crítico:
      • Las frecuencias observadas se alejan de las esperadas
      • Rechace la hipótesis nula a favor de la hipótesis alternativa basándose en este nivel α.
    • Si el resultado calculado de la prueba estadística < valor crítico:
      • Las frecuencias observadas se acercan a las esperadas
      • No rechace la hipótesis nula basándose en este nivel α.
Ejemplo de tabla de chi-cuadrado

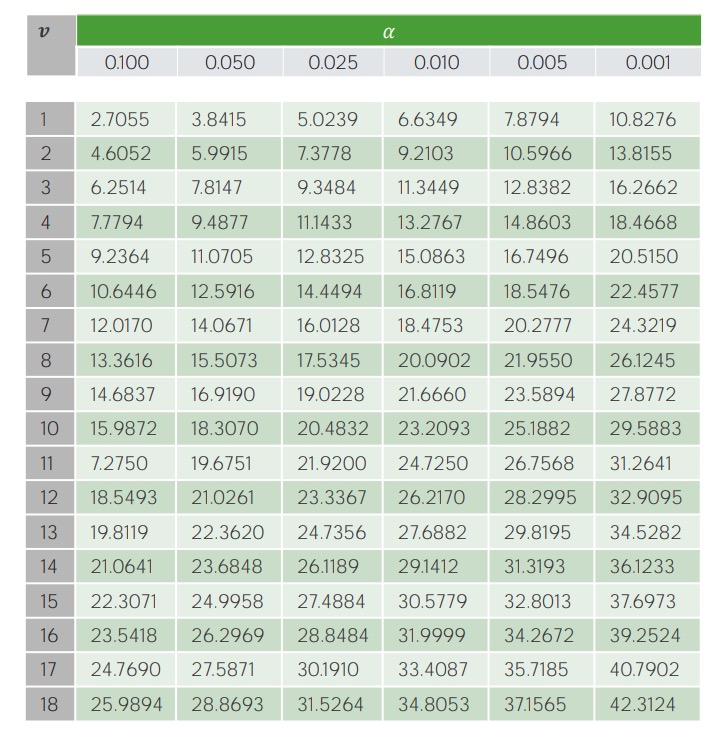
Ejemplo de la tabla de valores críticos para la prueba 𝝌2:
En el eje Y, V representa los grados de libertad (i.e., el número de categorías estudiadas menos 1); los niveles de significancia (niveles α) se muestran en el eje X. Los valores críticos correspondientes se encuentran en la tabla y se comparan con el resultado calculado de la prueba estadística.

Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0

Ejemplo de prueba 𝝌2: ¿Tienen los malabaristas más probabilidades de nacer en una determinada estación del año a un nivel de significancia de 0,05?

  • Hay 4 estaciones diferentes, por lo que hay 3 grados de libertad.
  • Nivel α = 0,05
  • Utilizando la tabla anterior, el número crítico es 7,81
  • Por lo tanto, rechazaremos nuestra hipótesis nula si el resultado calculado de la prueba estadística es > 7,81.
Cálculos asumiendo que la frecuencia esperada en cada celda es de 75
Categoría (i): temporada de nacimiento Frecuencia observada de malabaristas con cada estación de nacimiento (Observado – esperado)2/esperado
Primavera 66 (66 ‒ 75)2 / 75 = 1,08
Verano 82 (82 ‒ 75)2 / 75 = 0,653
Otoño 74 (74 ‒ 75)2 / 75 = 0,013
Invierno 78 (78 ‒ 75)2 / 75 = 0,12

𝝌2= 1,08 + 0,653 + 0,013 + 0,12 = 1,866

Como 1,866 es < 7,81 (nuestro valor crítico), tenemos que no rechazar (i.e., aceptar) la hipótesis nula y concluir que la estación de nacimiento no está asociada con el nacimiento de malabaristas.

Errores comunes:

  • No utilice el chi-cuadrado a menos que los datos sean cuantificables.
  • Tenga cuidado con los tamaños de muestra grandes, ya que los grados de libertad no aumentan.

Prueba exacta de Fisher

Similar a la prueba 𝝌2, la prueba exacta de Fisher es una prueba estadística utilizada para determinar si existen asociaciones no aleatorias entre 2 variables categóricas.

  • Se utiliza para analizar los datos encontrados en las tablas de contingencia y determinar la desviación de los datos respecto a la hipótesis nula (i.e., el valor p)
    • Por ejemplo: comparar 2 posibles “exposiciones” (fumar frente a no fumar) con 2 posibles resultados (desarrollar cáncer de pulmón frente a estar sano)
    • Las tablas de contingencia pueden tener > 2 “exposiciones” o > 2 resultados
  • Más preciso para conjuntos de datos pequeños
  • La prueba de Fisher proporciona valores p exactos basados en la tabla.
  • Fórmula complicada para calcular el resultado de la prueba estadística, por lo que suele calcularse con software.

Una tabla de contingencia 2 × 2 se establece así:

Y Z Total de filas
W A B A + B
X C D C + D
Total de la columna A + C B + D A + B + C + D (= n)

El resultado de la prueba estadística, p, se calcula a partir de esta tabla mediante la siguiente fórmula:

$$ p = \frac{(\frac{a+b}{a})(\frac{c+d}{c})}{(\frac{n}{a+c})} = \frac{(\frac{a+b}{b})(\frac{c+d}{d})}{(\frac{n}{b+d})} = \frac{(a+b)! (c+d)! (a+c)! (b+d)!}{a! b! c! d! n!} $$

donde p = valor p; A, B, C y D son números de las celdas de una tabla de contingencia básica de 2 × 2; y n = total de A + B + C + D.

Videos relevantes

14:43
Categorical Data Analysis

Representación Gráfica de los Datos

Propósito

Antes de realizar cualquier cálculo, los datos deben presentarse en un formato gráfico sencillo (e.g., gráfico de barras, diagrama de dispersión, histograma).

  • Las características de la distribución de los datos indicarán las herramientas estadísticas que se necesitarán para el análisis.
  • Los gráficos son el 1er paso en el análisis de datos, ya que permiten la visualización inmediata de distribuciones y patrones, que determinarán los siguientes pasos del análisis estadístico.
  • Los valores atípicos pueden ser una indicación de errores matemáticos o experimentales.
  • Hay muchas formas de representar gráficamente los datos.
  • Una vez realizados los cálculos, la presentación visual puede ayudar al lector a conceptualizar los resultados.

Visualización de una relación entre variables

Tablas de contingencia:

  • Tablas que muestran las frecuencias relativas de diferentes combinaciones de variables
  • Ejemplo: la comparación de los resultados de una prueba de tamizaje (positiva o negativa) con el hecho de que las personas tengan o no una enfermedad. (Nota: este tipo específico de tabla de contingencia puede utilizarse para calcular la sensibilidad y la especificidad de una prueba de tamizaje).
Tabla de contingencia para falsos positivos y negativos

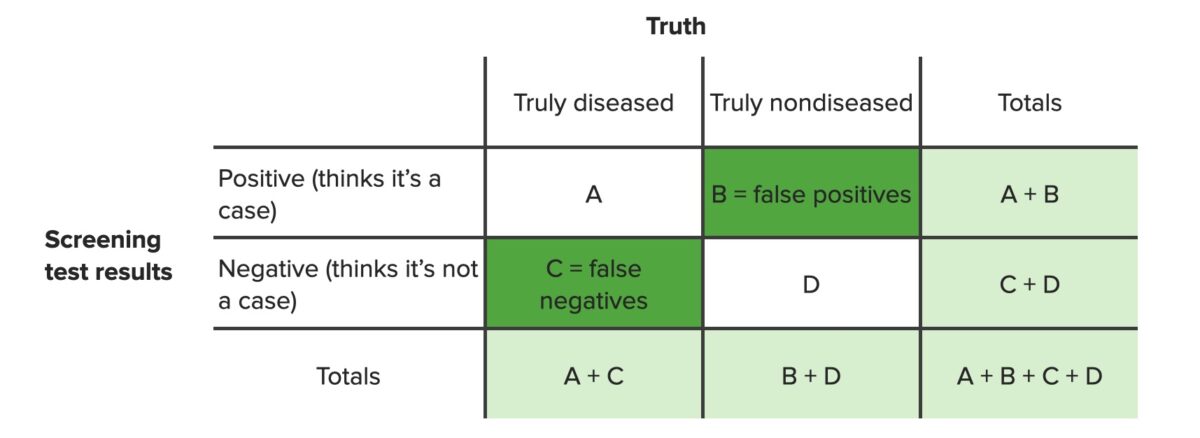
Tabla de contingencia que identifica los falsos positivos (b) y los falsos negativos (c)

Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0

Diagramas de dispersión:

  • Método comúnmente utilizado para mostrar la relación entre 2 variables numéricas o 1 variable numérica y 1 variable categórica
  • Los puntos representan los valores de los datos individuales.
  • Permite calcular una “línea de mejor ajuste” que representa los datos en su conjunto
  • Permite visualizar fácilmente todo el conjunto de datos
  • Ejemplo: diagrama de dispersión que muestra la relación entre 2 variables numéricas
Gráfico de dispersión

Ejemplo de diagrama de dispersión

Imagen: “Scatterplot” por Qwertyus. Licencia: CC0 1.0

Gráficos de cuadros:

  • Muestra la dispersión y los centros del conjunto de datos
  • Expresa visualmente un resumen de 5 números:
    1. El valor mínimo se muestra al final de la izquierda del cuadro.
    2. El primer cuartil (Q1) está en el extremo izquierdo del cuadro.
    3. La media se muestra como la línea en el centro del cuadro
    4. El tercer cuartil (Q3) está en el extremo derecho del cuadro.
    5. El valor máximo se muestra al final de la derecha del cuadro.
  • Se utiliza normalmente cuando se comparan las medias y las distribuciones entre 2 poblaciones
  • Ejemplo: el siguiente gráfico de cuadros compara los periodos de incubación medios entre las diferentes variantes del nuevo coronavirus, el síndrome agudo respiratorio severo (SARS) y el síndrome respiratorio de Oriente Medio (MERS, en inglés).
Gráfico de caja del periodo de incubación del sars-cov-2

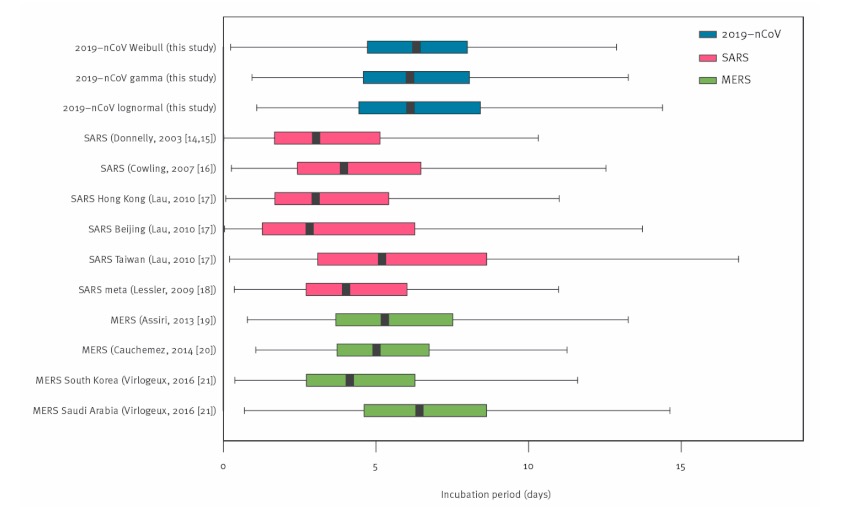
Ejemplo de gráfico de cuadros

Imagen: “Box-and-whisker-plots” por Jantien A. Backer, Don Klinkenberg, Jacco Wallinga. Licencia: CC BY 4.0

Curvas de supervivencia de Kaplan-Meier

  • Un tipo de análisis estadístico utilizado para estimar los datos del tiempo hasta el acontecimiento—típicamente, datos de supervivencia-.
  • Se utiliza habitualmente en los estudios médicos que muestran cómo un determinado tratamiento puede afectar o prolongar la supervivencia.
  • La línea representa el número de pacientes que sobreviven (o que aún no han alcanzado un determinado punto final) en un momento determinado.
  • Ejemplo: la curva de supervivencia que aparece a continuación muestra cómo afectan a la supervivencia dos patrones genéticos diferentes. El estudio comienza en el punto de tiempo 0, con el 100% de los 2 grupos sobreviviendo. Cada descenso en la línea representa la muerte de personas en cada grupo, lo que disminuye el porcentaje de personas que siguen viviendo. Después de 3 años, aproximadamente el 50% de las personas con la presencia del gen A siguen vivas, en comparación con solo el 5% que tienen la presencia del gen B.
Ejemplo de gráfico de kaplan-meier

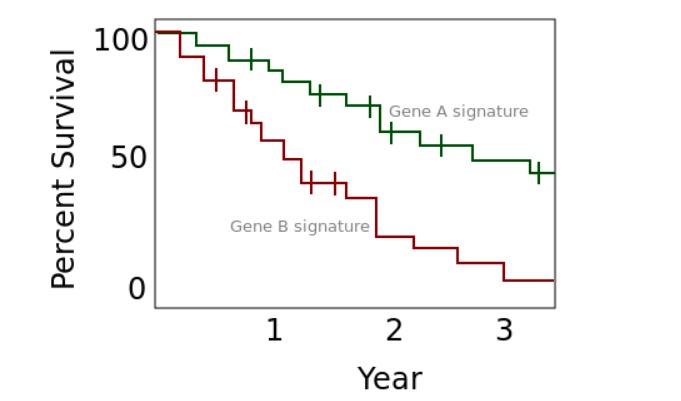
Ejemplo de gráfico de Kaplan-Meier

Imagen: “An example of a Kaplan Meier plot” por Rw251. Licencia: CC0 1.0

Presentación de las variables numéricas

Tablas (una tabla de frecuencias es 1 ejemplo):

  • La forma más sencilla de graficar datos
  • Los datos se muestran en columnas y filas.

Histogramas:

  • Es bueno para demostrar los resultados de los datos continuos, como:
    • Pesos
    • Alturas
    • Duración
  • Similar, pero no igual, a los gráficos de barras (que muestran datos categóricos)
  • La visualización de un histograma divide los datos continuos en intervalos o rangos.
  • La altura de cada barra representa el número de datos que entran en ese rango.
  • Como los histogramas representan datos continuos, se dibujan sin espacios entre barras.
  • Ejemplo: un histograma que muestra cuántas personas perdieron o ganaron peso durante un período de estudio de 2 semanas. En este ejemplo, 1 persona perdió entre 2,5 y 3 libras, 27 personas ganaron entre 0 y 0,5 libras, y 6 personas ganaron entre 1 y 1,5 libras.
Ejemplo de histograma

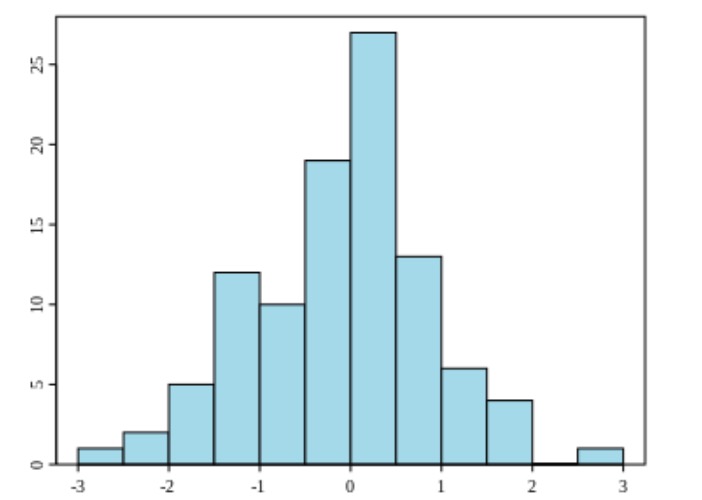
Ejemplo de histograma

Imagen: “Example of a histogram” por Jkv. Licencia: Dominio Público

Gráficos de polígonos de frecuencia:

  • Un gráfico de polígono de frecuencias traza las frecuencias de cada dato (o rango en un histograma) y las conecta con una línea.
  • Bueno para entender la forma de una distribución
Ejemplo de gráfico de polígono de frecuencias

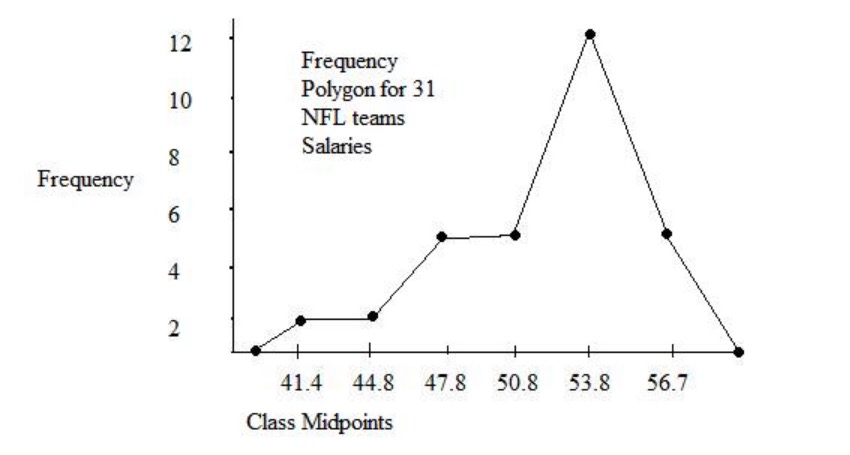
Gráfico de polígonos de frecuencia para los salarios de 31 equipos de la Liga de Fútbol Nacional (NFL, por sus siglas en inglés)

Imagen: “Example of a frequency polygon chart” por JLW87. Licencia: Dominio Público

Presentación de las variables categóricas

Las tablas de frecuencia, los gráficos de barras/histogramas y los gráficos circulares son tres de las formas más comunes de presentar datos categóricos.

Tablas de frecuencia:

  • Muestran números y/o porcentajes para cada valor de una variable
  • Ejemplo: acercarse a 100 semáforos diferentes y registrar si el semáforo estaba en rojo, amarillo o verde a la llegada.
Tabla: ejemplo de tabla de frecuencias
Color del semáforo Frecuencia
Rojo 65
Amarillo 5
Verde 30

Gráfico de barras:

  • La longitud de cada barra indica el número o la frecuencia de esa variable en el conjunto de datos; las barras pueden representarse vertical u horizontalmente
  • Ejemplo: un gráfico de barras que muestra el desglose de la raza/etnia en Texas en 2015.
Ejemplo de gráfico de barras

Ejemplo de gráfico de barras

Imagen: “Bar Chart of Race & Ethnicity in Texas” por Datawheel. Licencia: CC0 1.0

Gráficos circulares:

  • Demuestra las proporciones relativas entre diferentes variables categóricas
  • Ejemplo: el siguiente gráfico circular muestra los resultados de las elecciones al Parlamento Europeo de 2004, en el que cada color representa un partido político diferente y el porcentaje de votos que recibió.
Ejemplo de gráfico circular

Ejemplo de gráfico circular

Imagen: “A pie chart for the example data” por Liftarn. Licencia: Dominio Público

Referencias

  1. Greenhalgh, T. (2014). How to Read a Paper: The Basics of Evidence-Based Medicine. Chichester, UK: Wiley.
  2. Cochran, W. G. (1952). The chi-square test of goodness of fit. Annals of Mathematical Statistics 23(3):315–345.
  3. Yates, F. (1934). Contingency table involving small numbers and the χ2 test. Supplement to the Journal of the Royal Statistical Society 1(2):217–235.
  4. Kale, A. (2009). Chapter 2 of Basics of Research Methodology. Essentials of Research Methodology and Dissertation Writing, 7–14.
  5. Till, Y., Matei, A. (n.d.). Basics of Sampling for Survey Research. SAGE Handbook of Survey Methodology, pp. 311–328.
  6. Shober, P. et al. (2018). Statistical significance versus clinical importance of observed effect sizes: what do p values and confidence intervals really represent? Anesthesia & Analgesia 126:1068–1072.
  7. Katz, D. L., et al. (Eds.), Jekel’s Epidemiology, Biostatistics, Preventive Medicine, and Public Health, pp. 105–118. Retrieved July 8, 2021, from https://search.library.uq.edu.au/primo-explore/fulldisplay?vid=61UQ&search_scope=61UQ_All&tab=61uq_all&docid=61UQ_ALMA2193525390003131&lang=en_US&context=L

2024 Lecturio GmbH. Todos los derechos reservados.

USMLE™ es un programa conjunto de la Federation of State Medical Boards (FSMB®) y la National Board of Medical Examiners (NBME®). MCAT es una marca registrada de la Association of American Medical Colleges (AAMC). NCLEX®, NCLEX-RN® y NCLEX-PN® son marcas registradas del National Council of State Boards of Nursing, Inc (NCSBN®). Ninguno de los titulares de las marcas registradas está avalado ni afiliado a Lecturio.

¡Crea tu cuenta gratis o inicia una sesión para seguir leyendo!

Regístrate ahora y obtén acceso gratuito a Lecturio con páginas de concepto, videos médicos y cuestionarios para tu educación médica.

INICIA UNA SESIÓN EN TU CUENTA

User Reviews

Details