La tendencia central es una medida de los valores de una muestra que identifica los diferentes puntos centrales de los datos, a menudo denominados coloquialmente “promedios”. Las medidas de tendencia central más comunes son la media, la mediana y la moda. La identificación del valor central permite comparar otros valores con él, mostrando la dispersión o agrupación de la muestra, lo que se conoce como dispersión o distribución. Estas medidas de dispersión se clasifican en 2 grupos: medidas de dispersión basadas en los percentiles y medidas de dispersión basadas en la media (lo que se conoce comúnmente como desviaciones estándar). El análisis de la distribución de los datos determina si los datos tienen una tendencia central fuerte o débil en función de su dispersión. Cuando la distribución de los datos es simétrica y la media = la mediana = la moda, se dice que los datos tienen una distribución normal. También son posibles otros tipos de distribuciones, que se conocen como distribuciones no normales.
Última actualización: Jul 28, 2022
Las medidas de tendencia central son valores únicos que intentan describir un conjunto de datos identificando el valor central o “típico” de ese conjunto de datos.
Definición:
La media es la suma de todas las mediciones de un conjunto de datos dividida por el número de mediciones de ese conjunto.
Ecuación:
$$ Media = \frac{Suma\ de\ todos\ los\ valores\ en\ el\ conjunto}{Número\ total\ de\ valores\ en\ el\ conjunto} $$ $$ Media = \frac{x_{1}+x_{2}+x_{3}+…+x_{n}}{n} $$Ejemplo:
Encuentra la media del siguiente conjunto de datos: 1, 1, 1, 3, 5, 5, 7, 19.
Respuesta: hay 8 números en este conjunto de datos. Para calcular la media, sume todos los números y divídalos entre 8:
$$ Media = \frac{1+1+1+3+5+5+7+19}{8}=\frac{42}{8}=5.25 $$Definición:
Tras ordenar los datos de menor a mayor, la mediana es el valor medio, que separa la mitad inferior de la superior del conjunto de datos.
Ecuación:
Para encontrar la mediana, ordene los valores de menor a mayor, y luego utiliza la siguiente ecuación para determinar qué “posición” en el orden representa la mediana:
$$ Median = \left \{ \frac{(n+1)}{2} \right \} $$donde n = el número de valores del conjunto de datos.
Ejemplo:
Encuentra la mediana del siguiente conjunto de datos: 1, 5, 1, 19, 3, 1, 7, 5.
Respuesta: hay 8 números en este conjunto de datos. Para hallar la mediana, primero hay que ordenar los números: 1, 1, 1, 3, 5, 5, 7, 19. A continuación, determine qué “posición” representa la mediana. Para ello, utilice la fórmula (n + 1) / 2. Hay 8 números en este conjunto de datos, por lo que n = 8. Por lo tanto, la mediana será (8 + 1) / 2 = 4,5. La mediana está entre los números 4to y 5to, que son 3 y 5 (visualmente: 1, 1, 1, 3, 5, 5, 7, 19). Así que la mediana en este conjunto de datos es 4.
Definición:
La moda es el valor que aparece con mayor frecuencia en el conjunto de datos.
Ejemplo:
Encuentra la moda del siguiente conjunto de datos: 1, 5, 1, 19, 3, 1, 7, 5.
Respuesta: identifique el número que aparece más veces. Para ello, se puede establecer una tabla de frecuencias:
| Datos | Frecuencia (la frecuencia con la que se produce el punto de datos en la muestra) |
|---|---|
| 1 | 3 |
| 3 | 1 |
| 5 | 2 |
| 7 | 1 |
| 19 | 1 |
| Tipo | Descripción | Ejemplo | Resultado |
|---|---|---|---|
| Media | Suma total de los valores dividida por el número de valores | (8 + 4 + 10 + 4 + 4 + 5 + 4 + 5 + 6) / 9 | 5.5 |
| Mediana | Valor medio que separa la mitad superior de la inferior | 4, 4, 4, 4, 5, 5, 6, 8, 10 | 5 |
| Moda | Número más frecuente | 4, 4, 4, 4, 5, 5, 6, 8, 10 | 4 |
La dispersión es la amplitud de la distribución de los valores en un conjunto de datos. Varias medidas de dispersión incluyen un rango, cuantiles (e.g., cuartiles o percentiles) y desviaciones estándar.
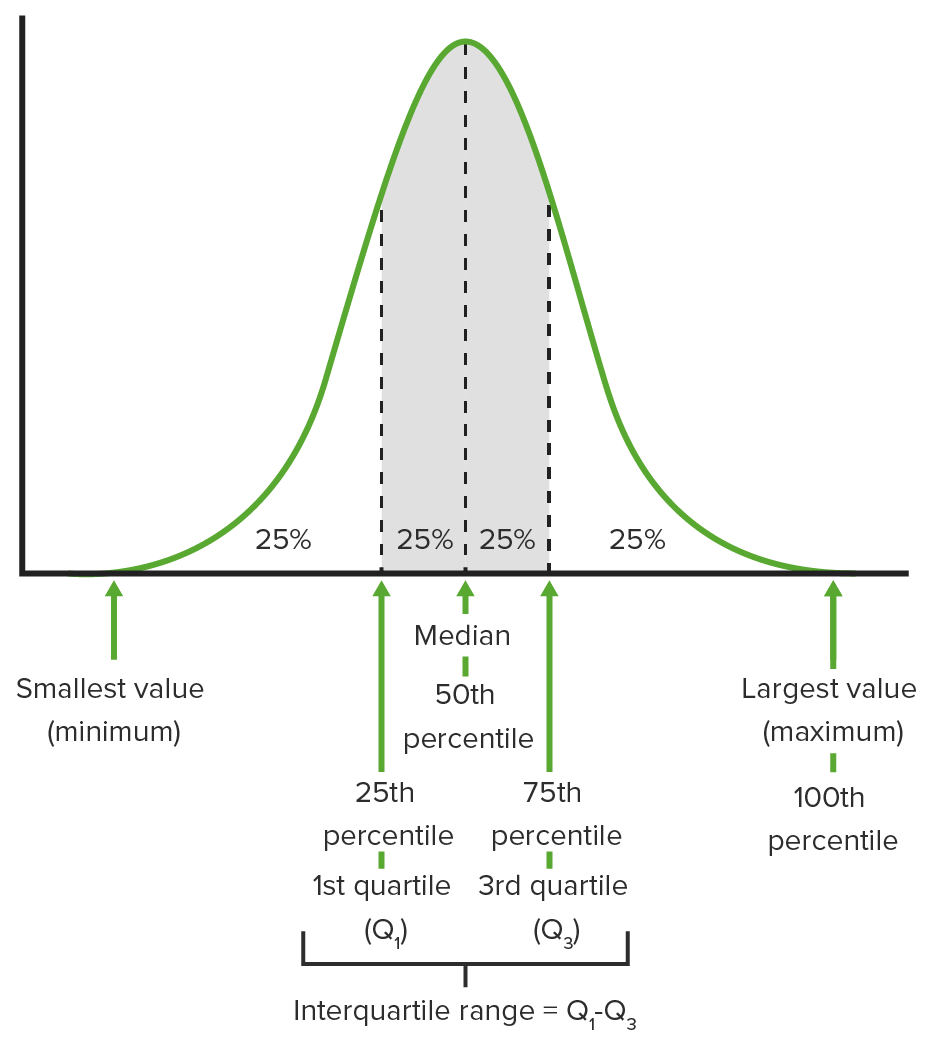
Representación gráfica de los cuartiles, los percentiles importantes y el rango intercuartílico
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0Definición: la desviación estándar es una medida de la distancia que hay entre cada valor observado y la media en un conjunto de datos.
Demostración de los porcentajes asociados a cada desviación estándar de la media:
Cuanto más “plana” sea la campana, más dispersos estarán los datos en el conjunto y, por tanto, mayores serán las desviaciones estándar calculadas.
Ecuación:
Matemáticamente, la DE puede calcularse mediante la siguiente ecuación:
$$ \sigma = \sqrt{\frac{\sum (\chi _{i}-\mu )^{2}}{N}} $$σ = desviación estándar de la población
Ν = el tamaño de la población
χᵢ = cada valor de la población
μ = la media de la población
Cálculos (utilizando la ecuación):
La distribución de los datos describe cómo se agrupan (o no se agrupan) los datos. Los datos tienden a agruparse en determinados patrones, conocidos como patrones de distribución. Hay un patrón de distribución “normal” y hay múltiples patrones no normales. Se utilizan diferentes pruebas estadísticas para diferentes patrones de distribución.
Las distribuciones normales difieren según su media y varianza, pero comparten las siguientes características:
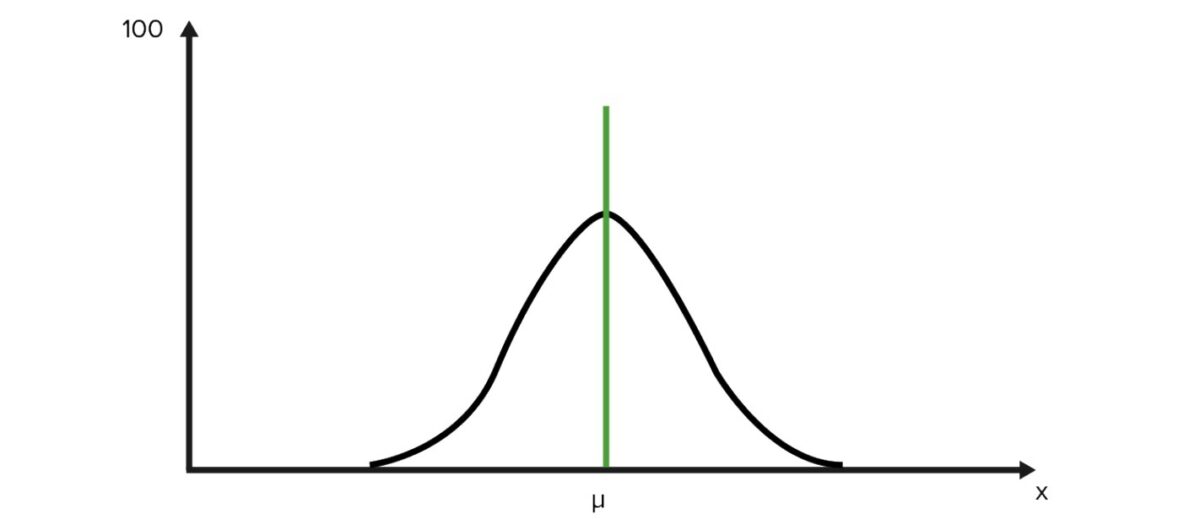
Ejemplo de distribución normal
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0Muchos procesos siguen una distribución no normal, que puede deberse a las variaciones naturales o a los errores de los datos.
Distribuciones comunes:
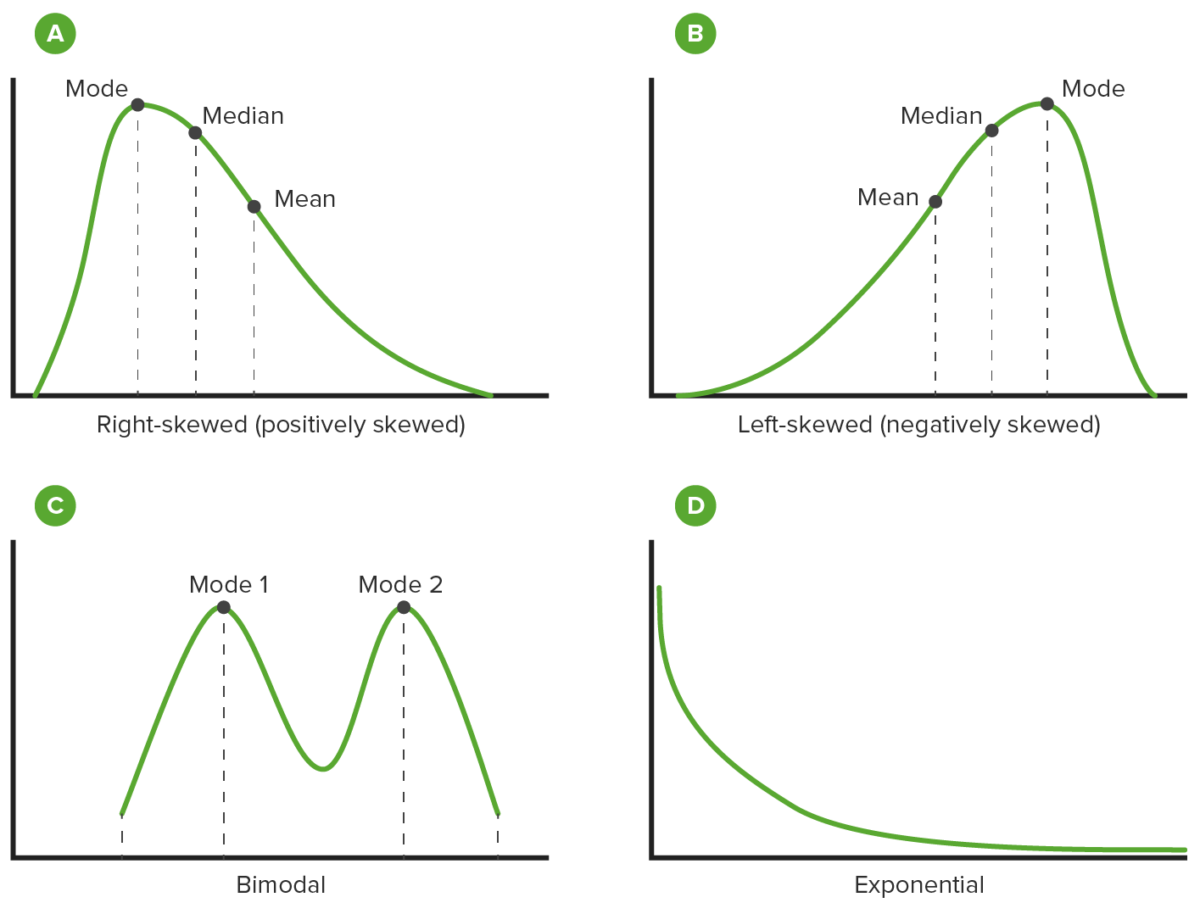
Tipos de distribuciones no normales
Imagen por Lecturio. Licencia: CC BY-NC-SA 4.0Razones por las que los datos pueden tener una distribución no normal:
USMLE™ es un programa conjunto de la Federation of State Medical Boards (FSMB®) y la National Board of Medical Examiners (NBME®). MCAT es una marca registrada de la Association of American Medical Colleges (AAMC). NCLEX®, NCLEX-RN® y NCLEX-PN® son marcas registradas del National Council of State Boards of Nursing, Inc (NCSBN®). Ninguno de los titulares de las marcas registradas está avalado ni afiliado a Lecturio.
Regístrate ahora y obtén acceso gratuito a Lecturio con páginas de concepto, videos médicos y cuestionarios para tu educación médica.