Los LOS Neisseria datos epidemiológicos obtenidos mediante estudios clínicos permiten a los LOS Neisseria investigadores determinar la probabilidad de desarrollar un determinado resultado de interés dentro de una población estudiada. Esta probabilidad, o riesgo, se puede cuantificar a través de lo que se conoce como medidas de riesgo, que son fórmulas matemáticas derivadas de tablas de contingencia. Estas medidas de riesgo incluyen riesgo absoluto (RA), riesgo relativo ( RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk), riesgo atribuible y razones de probabilidad (RP), cada una de las cuales ofrece diferentes tipos de información según las necesidades de los LOS Neisseria investigadores.
Last updated: Dec 15, 2025
Una tabla de contingencia enumera las distribuciones de frecuencia de las variables de un estudio y es una forma conveniente de ver cualquier relación entre las variables.
A continuación se muestra un ejemplo de una tabla de contingencia de 2×2. Las celdas muestran las frecuencias de distribución (A, B, C, D) para diferentes combinaciones de las dos variables (resultado, exposición), para una población de tamaño N.
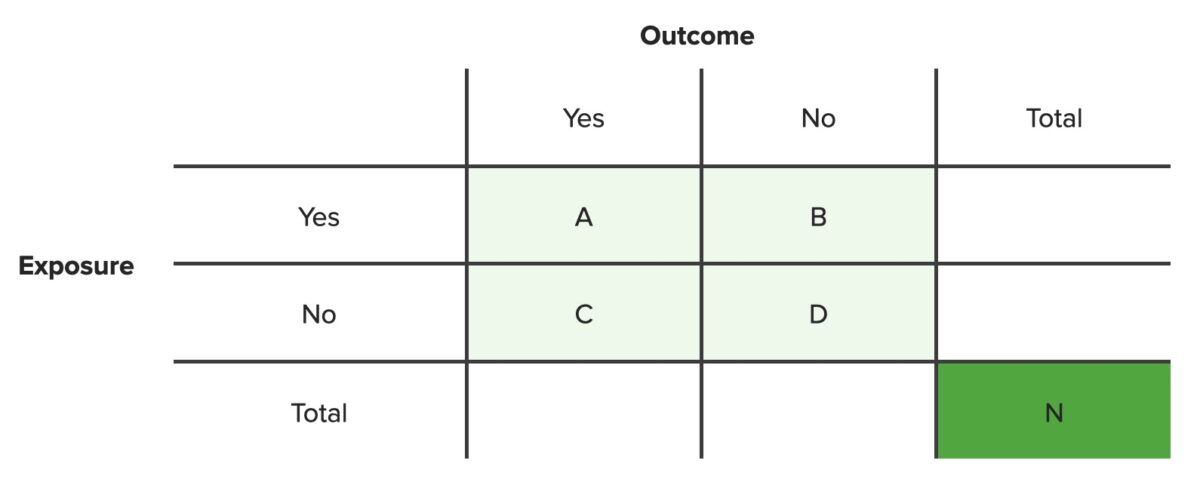
Tabla de contingencia
N = número total de personas en la población establecida
El RA es el riesgo de desarrollar una enfermedad o afección después de una exposición.
El RA se calcula como el número de personas que tienen un resultado particular, dividido por el número total de personas con la misma exposición (o la misma no exposición). Este riesgo se puede calcular tanto para las poblaciones expuestas como para las no expuestas.
Pasos:
Se comienza configurando una tabla de contingencia:

Tabla de contingencia
N = número total de personas en la población establecida
Usando la tabla de contingencia, el RA en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo expuesto se calcula como:
$$ Riesgo\ absoluto\ del\ grupo\ expuesto = \frac{A} {A + B} $$donde A = un paciente que estuvo expuesto al AL Amyloidosis factor de riesgo y desarrolló el resultado y B = un paciente que estuvo expuesto al AL Amyloidosis factor de riesgo pero no desarrolló el resultado.
Usando la tabla de contingencia, el RA en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo no expuesto se calcula como:
$$ Riesgo\ absoluto\ del\ grupo\ no expuesto = \frac{C} {C + D} $$donde C = un paciente que no estuvo expuesto al AL Amyloidosis factor de riesgo pero desarrolló el resultado de todos modos y D = un paciente que no estuvo expuesto al AL Amyloidosis factor de riesgo y no desarrolló el resultado.
Ejemplo 1: en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no. ¿Cuál es el RA de desarrollar cáncer de pulmón si eres fumador?
Ejemplo 2: en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. ¿Cuál es el RA de desarrollar cáncer de pulmón si no eres fumador?
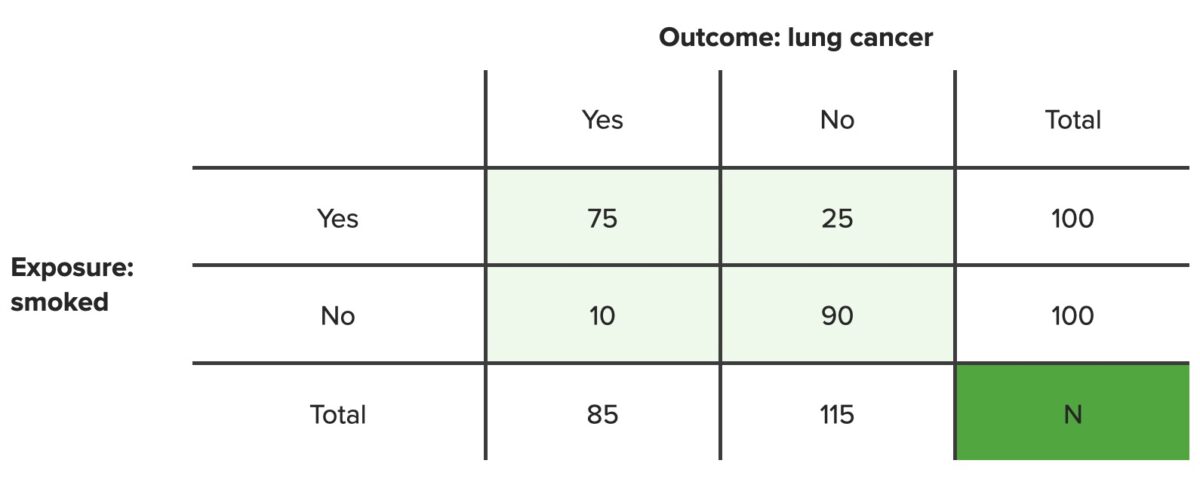
Tabla de contingencia
N = número total de personas en la población establecida
La RRA o el IRA es una medida de la reducción o incremento del riesgo de desarrollar una enfermedad o afección como resultado de una exposición.
Otras formas de conceptualizar la RRA:
La RRA puede interpretarse como la salud “ganada” o “perdida” como resultado de la exposición. Por ejemplo, si no fuma, ¿ en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum qué porcentaje puede reducir su riesgo de cáncer de pulmón?
La RRA entre los LOS Neisseria grupos expuesto y no expuesto se puede calcular como:
$$ RRA = I_{Expuesto} – I_{No expuesto} $$donde I = tasa de incidencia. Como I es lo mismo que RA, esta fórmula se puede calcular a partir de una tabla de contingencia:
$$ RRA = \frac{A} {A + B} – \frac{C} {C + D} $$En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. ¿ En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum cuánto no fumar reduce el RA de desarrollar cáncer de pulmón?

Tabla de contingencia
N = número total de personas en la población establecida
Estos son números típicamente reportados cuando se prueban nuevas opciones terapéuticas. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum estos casos:
Número necesario a tratar ( NNT NNT The number needed to treat (NNT) is the number of patients that are needed to treat to prevent 1 additional adverse outcome (e.g., stroke, death). For example, if a drug has an nnt of 10, it means 10 people must be treated with the drug to prevent 1 additional adverse outcome. Number Needed to Treat):
Número necesario para dañar (NND):
El riesgo relativo ( RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk) es el riesgo de que ocurra una enfermedad o afección en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo o población con una exposición particular en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum relación con un grupo de control (no expuesto).
El RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk es típicamente uno de los LOS Neisseria números más importantes calculados. Los LOS Neisseria estudios de cohortes son el único tipo de estudio observacional que pueda determinar el RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk.
El riesgo relativo se calcula como la frecuencia de una enfermedad o afección en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo expuesto (IE) dividida por la frecuencia en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo control no expuesto (IO), que se representa mediante la fórmula:
$$ RR = \frac{I_{E} }{I_{O} } $$Nuevamente, dado que las tasas de incidencia son las mismas que el RA, el RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk se puede calcular a partir de una tabla de contingencia utilizando la siguiente fórmula expandida:
$$ RR = \frac{\frac{A} {A + B}}{\frac{C} {C + D}} $$En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. ¿Cuál es el riesgo de contraer cáncer de pulmón si fuma en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum comparación con el riesgo de contraer cáncer de pulmón si no fuma?

Tabla de contingencia
N = número total de personas en la población establecida
Definición:
Cálculo:
La RRR RRR Measures of Risk se calcula como la diferencia entre la incidencia de una enfermedad en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un grupo expuesto (IE) y no expuesto (IO), dividida por la incidencia en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum el grupo no expuesto, que se calcula con la siguiente fórmula:
$$ RRR = \frac{RRA}{I_{O}} = (\frac{I_{E} – I_{O}}{I_{O}}) = \frac{\frac{A}{A + B} – \frac{C}{C + D}}{\frac{C}{C + D}} $$En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no después de 10 años en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un estudio de cohortes. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. Si la gente no fumase, ¿cuánto menos cáncer de pulmón se puede esperar en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la población?

Tabla de contingencia
N = número total de personas en la población establecida
El riesgo atribuible es una medida del riesgo de desarrollar un resultado asociado con una exposición particular.
El riesgo atribuible
en
EN
Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins.
Erythema Nodosum el grupo expuesto es la diferencia
en
EN
Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins.
Erythema Nodosum la tasa de una enfermedad entre
los
LOS
Neisseria grupos expuestos y no expuestos. Por ejemplo, ¿qué porcentaje de casos de cáncer de pulmón probablemente se deban
al
AL
Amyloidosis tabaquismo?
El riesgo atribuible se calcula restando la incidencia
en
EN
Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins.
Erythema Nodosum el grupo no expuesto (IO) de la incidencia del grupo expuesto (IE) y dividiendo por la incidencia
en
EN
Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins.
Erythema Nodosum el grupo expuesto, que se expresa como:
Ejemplo: en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no después de 10 años en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un estudio de cohortes. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. ¿Qué porcentaje de casos de cáncer de pulmón es probable que se deba al AL Amyloidosis tabaquismo?

Tabla de contingencia
N = número total de personas en la población establecida
El RAP es el riesgo atribuible para toda una población. Representa la fracción de casos que no ocurrirían en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población si se eliminara la exposición.
Por ejemplo, ¿qué porcentaje de casos de cáncer de pulmón se podrían prevenir si nadie fumara?
El RAP se calcula restando la tasa de incidencia en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la población no expuesta de la tasa de incidencia en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum toda la población:
$$ RAP = \frac{(I_{T} – I_{O})}{I_{T}} = \frac{(\frac{A + C}{N} – \frac{C}{C + D})}{\frac{A + C}{N}} $$Ejemplo: en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 fumadores, 75 desarrollaron cáncer de pulmón y 25 no, después de 10 años en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un estudio de cohorte. En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum una población de 100 no fumadores, 10 desarrollaron cáncer de pulmón y 90 no. ¿Qué porcentaje de casos de cáncer de pulmón se podrían prevenir si nadie fumara?
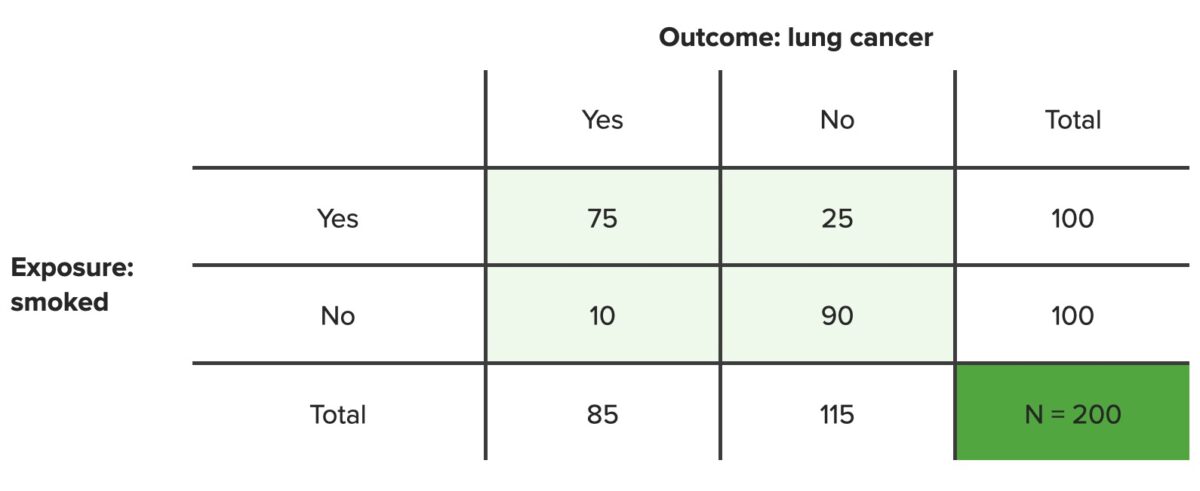
Tabla de contingencia
N = número total de personas en la población establecida
Una razón de probabilidades (RP) es una estadística que cuantifica la fuerza de asociación entre 2 variables o eventos.
Una RP se utiliza como una estimación de RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum estudios de casos y controles. La RP se calcula determinando las probabilidades de exposición entre los LOS Neisseria enfermos divididas por las probabilidades de exposición entre los LOS Neisseria no enfermos. Esto se representa como:
$$ RP = \frac{(Probabilidades\ de\ exposición\ entre\ enfermos)}{(Probabilidades\ de\ exposición\ entre\ no enfermos)} = \frac{A \div C}{B \div D} $$donde (A ÷ C) representa el número de casos expuestos dividido por el número de casos no expuestos entre aquellos con la enfermedad y (B ÷ D) es el número de enfermos expuestos dividido por el número de enfermos no expuestos.
Reorganizando la fórmula se obtiene la ecuación simplificada:
$$ RP = ( AD AD The term advance directive (AD) refers to treatment preferences and/or the designation of a surrogate decision-maker in the event that a person becomes unable to make medical decisions on their own behalf. Advance directives represent the ethical principle of autonomy and may take the form of a living will, health care proxy, durable power of attorney for health care, and/or a physician’s order for life-sustaining treatment. Advance Directives) \div (BC) $$La RP se interpreta de la misma manera que el RR RR Relative risk (RR) is the risk of a disease or condition occurring in a group or population with a particular exposure relative to a control (unexposed) group. Measures of Risk:
En EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum este ejemplo, 6 personas desarrollaron la enfermedad de Creutzfeldt-Jakob; 3 de ellos comieron una cantidad significativa de carne de res y 3 de ellos no. Estos pacientes se compararon con una población control en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum un estudio de casos y controles; en EN Erythema nodosum is an immune-mediated panniculitis (inflammation of the subcutaneous fat) caused by a type IV (delayed-type) hypersensitivity reaction. It commonly manifests in young women as tender, erythematous nodules on the shins. Erythema Nodosum la población control de 10 personas, 4 de ellas comieron una cantidad significativa de carne de res y 6 de ellas no. ¿Cuáles son las probabilidades de desarrollar enfermedad de Creutzfeldt-Jakob después de comer una cantidad significativa de carne de res?
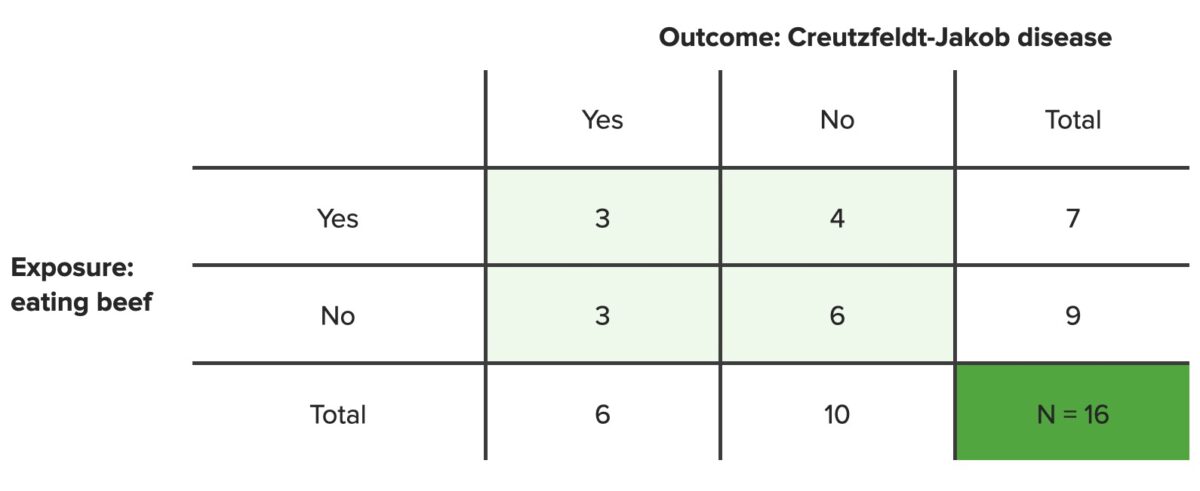
Tabla de contingencia
N = número total de personas en la población establecida
Nota: estos son datos hipotéticos; las verdaderas tasas de incidencia de la enfermedad de Creutzfeldt-Jakob son mucho más bajas de lo que sugieren estos datos.