Gases have low density and viscosity compared to other states of matter because the molecules in a gas are far apart from each other and are constantly moving in random directions. Boyle’s law states that at a constant temperature, the volume of a gas is inversely proportional to its pressure. Charles’s law states that at a constant pressure, the volume of a gas is directly proportional to its temperature. Henry’s law states that the amount of gas dissolved in a liquid is proportional to the pressure of the gas above the liquid, while the Van der Waals equation is a modified form of the ideal gas law that considers the effects of intermolecular forces and non-zero molecular volumes. Ideal gases obey the ideal gas law: the product of the pressure and volume of a gas is proportional to the number of molecules, the temperature, and the gas constant.
Last updated: Dec 15, 2025
Gases have low density and viscosity compared to other states of matter. Two laws explain their properties. Boyle’s law states that at a constant temperature, the pressure of the gas varies inversely with its volume. Charles’s law states that at constant pressure, the volume of the gas is directly proportional to its temperature. These laws explain the movement of gases in different body compartments.
| p | Pressure (Pa or N/m2) |
| F | Force acting on a surface (N) |
| A | Area of the surface, cross-section (m2) |
Liquids have no definite shape due to the mutual movement of molecules or atoms. They take the shape of the available vessel. As a whole, the surface of liquids forms a horizontal plane. In gases, there are no binding forces between the individual molecules. The molecules are–except at absolute 0–constantly in motion. If they collide or bounce against surrounding walls, they are repelled elastically. Thus, they move on irregular zigzag paths.
Gas molecule undergoes about 10 quadrillion collisions per second.
In a fully sealed vessel, the force can be exerted on a fluid utilizing a movable stamp. Unlike solids, where force can be exerted on one point, the particles of fluids can avoid contact due to their mobility. However, with a stamp, the force can act evenly throughout the entire surface of the stamp. Those particles that are adjacent to the surface of the stamp experience immediate pressure, which is then transferred in all directions due to their mobility. Therefore, the pressure is the same at any point within a fluid.
The pressure is defined as the ratio of a force applied perpendicular to a surface and the area of this surface: p = F/A
At constant temperature, the pressure of a gas is proportional to the number of molecules present in the respective area. Measure for the number of molecules is the mass Mass Three-dimensional lesion that occupies a space within the breast Imaging of the Breast of the gas.
At constant temperature and in a closed container, the product of pressure and volume of a given amount of gas is constant.
Since a change in pressure affects the volume of a gas, the density of gases must be pressure-dependent as well. At constant temperature, the density of a gas is proportional to the pressure. The behavior of density and pressure are the same.
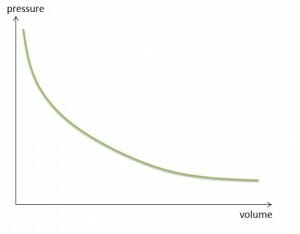
Boyle-Mariotte law: volume pressure
Image by Lecturio.The following conditions have been defined to simplify the calculation of gases:
| V | Volume (L) |
| m | Mass Mass Three-dimensional lesion that occupies a space within the breast Imaging of the Breast (kg) |
| M | Molar mass Mass Three-dimensional lesion that occupies a space within the breast Imaging of the Breast |
| n | Amount of substance (mol) |
| R | Universal gas constant [J/(K mol)] |
| T | Temperature (K or °C) |
For a description of ideal gases, a general equation of state (the ideal gas law) is used. It is defined as the simultaneous change of volume, pressure, and temperature.
$$ p V = m R T $$In this equation, absolute pressure must be used. The ideal gas law does not apply in conditions of overpressure. Furthermore, it only applies to ideal gases and has only limited validity Validity Validity refers to how accurate a test or research finding is. Causality, Validity, and Reliability in regard to real gases and none in regard to vapors. From the ideal gas law, a body’s standard volume can be calculated. Standard volume refers to the volume at standard atmospheric pressure Atmospheric pressure The pressure at any point in an atmosphere due solely to the weight of the atmospheric gases above the point concerned. Ventilation: Mechanics of Breathing p0 = 1013 mbar and at a temperature of T = 0°C. At these standard conditions (standard temperature and pressure or STP), 1 mole Mole Nevi (singular nevus), also known as “moles,” are benign neoplasms of the skin. Nevus is a non-specific medical term because it encompasses both congenital and acquired lesions, hyper- and hypopigmented lesions, and raised or flat lesions. Nevus/Nevi of an ideal gas occupies a volume of V0 = 22.4 L.
If the constant term pV PV Polycythemia vera (PV) is a chronic myeloproliferative neoplasm characterized by the overproduction of rbcs. In addition, the wbc and platelet counts are also increased, which differentiate pv from erythrocytosis seen with chronic hypoxia and other chronic conditions. Polycythemia Vera/T is proportional to the mass Mass Three-dimensional lesion that occupies a space within the breast Imaging of the Breast of the closed system, the associated proportionality factor is referred to as gas constant. The gas constant’s numerical value depends on the type of gas.
The number of similar particles contained in a system is described as the amount of a substance. Mole Mole Nevi (singular nevus), also known as “moles,” are benign neoplasms of the skin. Nevus is a non-specific medical term because it encompasses both congenital and acquired lesions, hyper- and hypopigmented lesions, and raised or flat lesions. Nevus/Nevi is the amount of a substance that contains as many particles as there are atoms in 12 grams of a carbon isotope C-12. So in all substances, an amount of 1 mole Mole Nevi (singular nevus), also known as “moles,” are benign neoplasms of the skin. Nevus is a non-specific medical term because it encompasses both congenital and acquired lesions, hyper- and hypopigmented lesions, and raised or flat lesions. Nevus/Nevi contains 6.0221367 x 1023 particles. At standard conditions, 1 mole Mole Nevi (singular nevus), also known as “moles,” are benign neoplasms of the skin. Nevus is a non-specific medical term because it encompasses both congenital and acquired lesions, hyper- and hypopigmented lesions, and raised or flat lesions. Nevus/Nevi of any gas has the same volume (see standard volume).
The product of universal gas constant with molar mass Mass Three-dimensional lesion that occupies a space within the breast Imaging of the Breast is called the molar gas constant. It is a universal constant and, thus, non-specific to substances.
$$ p V = n M R T $$The equation of state in relation to the amount of substance:
$$ p V = n R T $$Thus, the state of a gas is determined by 3 state variables (pressure, volume, temperature). Changes in 2 or all state variables are referred to as a change of state.
There is a clearly defined value of internal energy for each state of a system. To understand these changes, we recall the 1st law of thermodynamics:
The supply of heat Heat Inflammation and mechanical work increases the internal energy of a closed system. The following equation applies:
$$ ΔU = Q + W $$In ideal gases, mechanical work causes a volume change. The supplied thermal energy leads to an increase in internal energy and an increase in volume.
| Isothermal change of state |
|
| Isobaric change of state |
|
| Isochoric change of state |
|
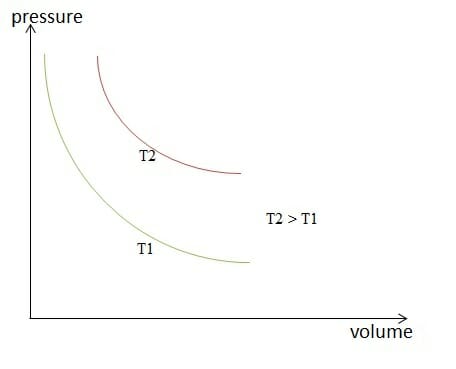
Isothermal change of state
Image by Lecturio.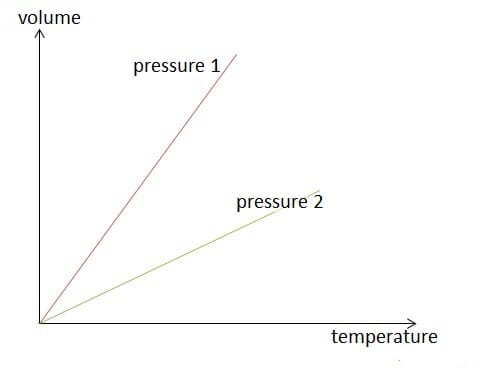
Isobaric change of state
Image by Lecturio.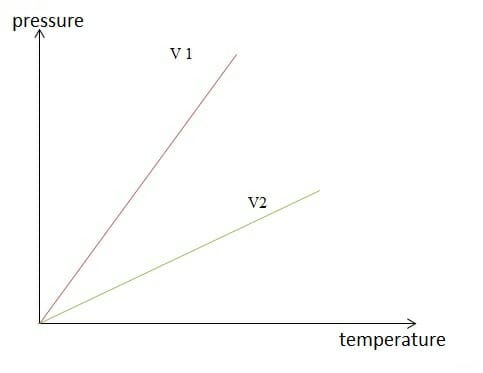
Isochoric change of state
Image by Lecturio.| K | Adiabatic exponent |
| ΔS | Change of entropy Entropy The measure of that part of the heat or energy of a system which is not available to perform work. Entropy increases in all natural (spontaneous and irreversible) processes. Enzyme Kinetics (S = 0 in adiabatic change) |
| Cp | Isobaric heat Heat Inflammation capacity [J/(kg K)] |
| CV | Isochoric heat Heat Inflammation capacity [J/(kg K)] |
Adiabatic change of an ideal gas takes place without heat Heat Inflammation exchange with the environment. Complete heat Heat Inflammation insulation is required for this change of state. Adiabatic changes of state are also referred to as isentropic changes of state. The corresponding equation for an isentropic change of state is the following:
$$pV^{K}= constant; K =\frac{C_{P}}{C_{V}}$$The work performed in an isentropic relaxation is only dependent on the change in temperature when the amount of gas is given.
Substances can assume the following states of aggregation Aggregation The attachment of platelets to one another. This clumping together can be induced by a number of agents (e.g., thrombin; collagen) and is part of the mechanism leading to the formation of a thrombus. Coagulation Studies:
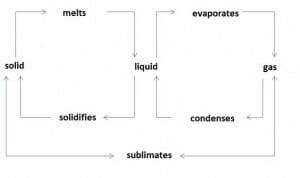
Overview physical state change
Image by Lecturio.Each of these 3 states of matter implies specific properties for a substance. Solid substances have a fixed shape and volume. Their particles are held together by cohesive forces. Liquid substances have no fixed shape. However, they have a fixed volume, and cohesive forces are acting between their particles. Gaseous substances neither possess a definite shape, nor a particular volume. Their particles exert only negligible cohesive forces.
To reach a higher state of aggregation Aggregation The attachment of platelets to one another. This clumping together can be induced by a number of agents (e.g., thrombin; collagen) and is part of the mechanism leading to the formation of a thrombus. Coagulation Studies (solid < liquid < gaseous), energy must be added. When a change into a lower state of aggregation Aggregation The attachment of platelets to one another. This clumping together can be induced by a number of agents (e.g., thrombin; collagen) and is part of the mechanism leading to the formation of a thrombus. Coagulation Studies takes place, energy is released.
The transition from a solid-state into a liquid state is called melting. The reverse change is called solidification.
Melting of a body occurs at its melting temperature. Melting and solidification temperatures are the same for a particular substance. During melting, the melting temperature remains constant despite the addition of heat Heat Inflammation. The added heat Heat Inflammation is used to transfer the substance from solid to liquid. The same applies to solidification: The temperature remains constant despite the release of heat Heat Inflammation. Only after the entire substance has solidified, further heat dissipation Heat Dissipation Heatstroke results in the cooling of the solid material.
Process in which a substance changes from a liquid to a gaseous state is called vaporization. The reverse process is called condensation.
There are 2 types of vaporization: Boiling implies the evaporation of a liquid where vapor bubbles form inside the liquid phase. The temperature of the liquid remains constant during boiling despite further heat Heat Inflammation supply. The boiling temperature is strongly dependent on the pressure of the liquid. Normal boiling temperature refers to the boiling temperature at atmospheric pressure Atmospheric pressure The pressure at any point in an atmosphere due solely to the weight of the atmospheric gases above the point concerned. Ventilation: Mechanics of Breathing of 1013 mbar. The other type of vaporization, where a liquid vaporizes below its boiling temperature, is called evaporation. It occurs only on the liquid surface and may occur at every temperature above 0. During evaporation, a liquid draws the required heat Heat Inflammation from its energy content and the environment.
Example: When a person is sweating, the sweat evaporates from the surface of the skin Skin The skin, also referred to as the integumentary system, is the largest organ of the body. The skin is primarily composed of the epidermis (outer layer) and dermis (deep layer). The epidermis is primarily composed of keratinocytes that undergo rapid turnover, while the dermis contains dense layers of connective tissue. Skin: Structure and Functions. The energy in the form of heat Heat Inflammation is released. The body gives off excess heat Heat Inflammation to prevent overheating.
Through evaporation and condensation of water, “pure” water can be produced. This type of liquid treatment is called distillation.
Many substances change directly from the solid to the gaseous state and vice versa, without any formation of a liquid. This phase transition from solid to gas, and vice versa, is called sublimation Sublimation A defense mechanism through which unacceptable impulses and instinctive urges are diverted into personally and socially acceptable channels; e.g., aggression may be diverted through sports activities. Defense Mechanisms and is observed in the volatilization of naphthalene or the formation of ice crystals in the air. The liquid state is skipped.
In the case of ideal gases, pressure and volume are inversely proportional to each other. In the case of real gases, this inverse proportionality is only accurate by approximation. When vapors change in volume, the pressure hardly changes at all. This difference between gases and vapors is based on the difference between the temperature and the pressure-dependent boiling point.
Vapor pressure Vapor pressure The contribution to barometric pressure of gaseous substance in equilibrium with its solid or liquid phase. Edema (p) does not depend on the volume of the vapor. It only depends on the temperature.
The vapor is saturated when the saturation vapor pressure Vapor pressure The contribution to barometric pressure of gaseous substance in equilibrium with its solid or liquid phase. Edema is reached, i.e. when it is in equilibrium Equilibrium Occurs when tumor cells survive the initial elimination attempt These cells are not able to progress, being maintained in a state of dormancy by the adaptive immune system. In this phase, tumor immunogenicity is edited, where T cells keep selectively attacking highly immunogenic tumor cells.This attack leaves other cells with less immunogenicity to potentially develop resistance to the immune response. Cancer Immunotherapy with the liquid’s pressure.
Gases are highly unsaturated vapors. Their temperature is far above the boiling point that corresponds to their pressure.
Since water constantly evaporates from the surface of all-natural bodies of water, the air always contains water vapor, which is mostly unsaturated. To become saturated, it must be cooled to a specific temperature, which is called the dew point. In case of cooling below the dew point, so much water vapor is condensed that only the water vapor content corresponding to this temperature remains. The condensed water vapor appears in the form of fog, rain, snow, or frost.
At each temperature, only a certain amount of water vapor can be contained in a specific volume of air. The water vapor content in the atmospheric air varies with time and location and is referred to as humidity. The maximum humidity is defined as the maximum amount of water vapor that can be contained in 1 cubic meter of air at a specific temperature.
$$F (maximum) =\frac{Mass~of~water~vapor~in~the~air}{Volume~of~humid~air}$$The critical temperature of a gas is the temperature at which liquefaction is no longer possible, regardless of how high the pressure is. The corresponding isothermal curve shows an inflection point with a horizontal tangent at the critical pressure. Only below the critical temperature, gases can be liquefied by applying pressure.
Real gases slightly cool down during a reduced relaxation.
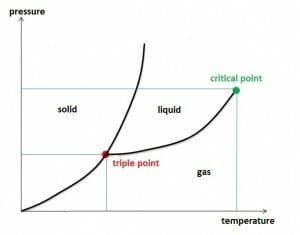
Triple point
Image by Lecturio.| pA | Partial pressure Partial pressure The pressure that would be exerted by one component of a mixture of gases if it were present alone in a container. Gas Exchange of a gas (bar) |
| A | Concentration of a gas in a solvent (mol/L) |
| K | Constant |
Mixtures of at least 2 different chemical elements that result in a gas are called gas mixtures. They have a homogeneous Homogeneous Imaging of the Spleen mixing ratio.
Henry’s law describes the solubility of a gas in a liquid. The gas concentration in the liquid is proportional to the partial pressure Partial pressure The pressure that would be exerted by one component of a mixture of gases if it were present alone in a container. Gas Exchange of the gas above the liquid.
$$A=K_{P_{A}}$$